Средняя линия треугольника соединяет середины двух сторон, параллельна третьей стороне и равна ее половине.
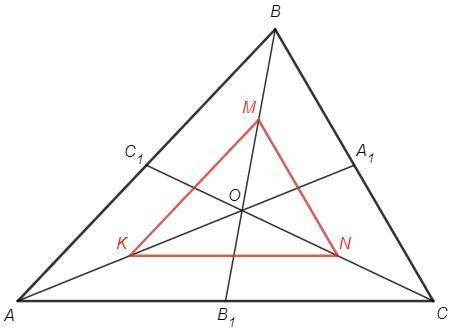
Отрезки KM, MN, KN являются средними линиями в треугольниках AOB, BOC, AOC.
a) KM||AB, MN||BC, KN||AC
KMN~ABC по трем параллельным сторонам
б) KM=AB/2, MN=BC/2, KN=AC/2
P(ABC) =2P(KMN) =44*2 =88 (см)
в) Отношение соответствующих отрезков (медиан, биссектрис, высот и любых отрезков, построенных сходным образом) в подобных треугольниках равно коэффициенту подобия.
k=AB/KM =2
Медианы ABC вдвое больше медиан KMN.
Расположим начало координат в точке А, ось Х вправо, ось Y вверх
А(0;0)
C(7;0)
Уравнение окружности радиусом 5 с началом в А
x²+y²=5²
Уравнение окружности радиусом 3√2 с началом в C
(x-7)²+y²=(3√2)²
Решаем совместно для нахождения координат точек В и Д
Вычтем из первого второе
x²-(x-7)²=5²-(3√2)²
14x-49=25-9*2
14x=49+25-18
14x=56
x=4
y²=5²-x²=25-16=9
y₁ = -3 - это точка Д(4;-3)
y₂ = +3 - это точка В(4;3)
Точка Ё - середина отрезка АВ, её координаты равны среднему арифметическому координат точек А и В
Ё = (А+В)/2 = ((0;0)+(4;3))/2 = (2;3/2)
Точка Щ - середина отрезка СД, её координаты равны среднему арифметическому координат точек С и Д
Щ = (С+Д)/2 = ((7;0)+(4;-3))/2 = (11/2;-3/2)
И расстояние ЁЩ
l² = (x₁-x₂)²+(y₁-y₂)²
l² = (2-11/2)²+(3/2+3/2)² = (7/2)²+(3)² = 49/4+9 = 85/4
l = √(85/4) = √85/2
И это ответ