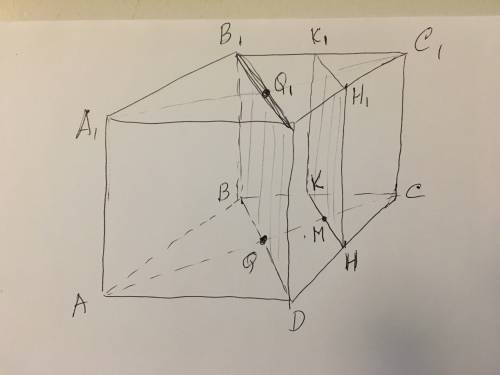
Построим сечение куба плоскостью проходящей через точки H (середина стороны DC), H1 (середина стороны D1C1) и M (середина отрезка CQ)
Соединим H с H1, продолжим отрезок HM до пересечения со стороной BC в точке K. Рассмотрев ΔBCD, видим, что отрезок HM проходит через середины стороны CD и высоты CQ, а следовательно KM является средней линией ΔBCD. Тогда K - середина стороны BC. Т.к. A1B1C1D1 || ABCD, то плоскость KHH1 пересекает их по параллельным прямым. Прямая параллельная KH и принадлежащая плоскости A1B1C1D1 и проходящая через точку H1 также будет средней линией K1H1, но в ΔC1B1D1.
Окончательно получаем в сечении прямоугольник KHH1K1.
Теперь построим сечение проходящее через точки Q, Q1 и D1
Проводим прямую через точки Q1 и D1 в плоскости A1B1C1D1 - это будет диагональ B1D1. Проводим прямую параллельную ей и принадлежащую плоскости ABCD и проходящую через точку Q - это будет диагональ BD. Окончательно получаем в сечении прямоугольник BDD1B1
BD || KH (KH - средняя линия ΔBCD)
BB1 || KK1 (KK1 - средняя линия квадрата BB1C1C)
BD пересекается с BB1 в точке B
KH пересекается с KK1 в точке K
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны ⇒ BDD1B1 || KHH1K1.
60°, 60°, 60°
Объяснение:
Дано АВСD - ромб, AM=BN, ∠BAD=60°.
Найти ∠DMN, ∠MND, ∠NDM.
Решение: ∠В=∠D=180-60=120°, т.к. сумма углов ромба, прилегающих к одной стороне, составляет 180°.
Проведем диагональ ВD. По свойству диагонали ромба, ∠АВD=∠DBC=60°. Значит, ∠АDB=60°, т.к. сумма углов треугольника составляет 180°
ΔАМD=ΔBND (AM=BN, AD=BD, ∠МАD=∠NBD), значит, DM=DN.
∠NDM=∠BDM+∠BDN=∠BDM+∠MDA=∠ADB=60°
Следовательно, ΔMND - равносторонний, ∠DMN=∠MND=∠NDM=60°.