Найдём односторонние углы берём угол А и угол В известно что сумма односторонних углов равна 180° 180°-85°(угол А)=95°(угол В) чтобы найти угол АВД вычитаем из угла В угол СВД 95°-65°=30°(угол АВД) найдем односторонние углы берём угол А и угол Д известно что сумма односторонних улов равно 180° 180°-85°=95°(угол Д) чтобы найти угол ВДС вычитаем из угла Д угол АДВ 95°-30°=65°(угол ВДС) нам известно что сумма углов четырёхугольника равна 360°, чтобы найти угол С, нам нужно сложить угла А, В, Д, и их сумму вычесть из 360° 85°(угол А)+95°(угол В)+95(угол Д)=275°(А+В+Д) 360°-275°=85°(угол С) ответ: угол С-85° угол АВД-30° угол ВДС-65°
Пусть данная пирамида МАВС, МО - высота, точка О - центр треугольника; угол ОМА=45°
МО⊥плоскости основания, ∆ МОА - прямоугольный.
Сумма острых углов прямоугольного треугольника 90°, ⇒∠МАО=45°,
∆ АОМ - равнобедренный. АО=МО=12 см.
О - точка пересечения медиан ∆ АВС, и по свойству медианы АО:НО=2:1. Тогда высота основания АН=12:2•3=18 см
АС=АН:sin 60°=18:√3/2=36:√3•2=12√3
V=S•h:3
Формула площади правильного треугольника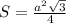
V=36•3•√3•12:3=432√3 см³
* * *
Объём цилиндра равен произведению площади основания на высоту. Пусть основание вписанной призмы – ∆ АВС, АВ - гипотенуза, АС =m, угол АВС=f.
.Центр окружности, описанной вокруг прямоугольного треугольника, лежит в середине гипотенузы, а радиус равен её половине.
⇒ радиус основания цилиндра равен половине АВ.
АВ=m:sin f
R=0,5m:sin f
V=πr²•h