1) Если все боковые стороны (это рёбра) пирамиды имеют одинаковую длину, то их проекции на основание - радиусы R описанной окружности вокруг основания.
Радиус равен половине диагонали основания.
R = √(3² + 4²) = 5 см.
Тогда высота Н пирамиды равна:
Н = √(13² - 5²) = √(169 - 25) = 12 см.
2) Будем считать, что в задании имеется в виду, что высота пирамиды проецируется на основание в вершину прямого угла.
Тогда 2 боковых грани пирамиды вертикальны, одна - наклонная.
Гипотенуза основания равна √(9² + 12²) = 15 см.
Высота основания на гипотенузу равна (9*12)/15 = (36/5) = 7,2 см.
Высота наклонной боковой грани равна √(8² + 7,2²) = 0,8√181 ≈ 10,7629 см.
Теперь можно определить площади боковых граней.
Sбок = (1/2) *(6*8 + 12*8 + 15*(4/5)√181) = (72 + 6√181) см².
Площадь основания Sо = (1/2)(9*12) = 54 см².
Полная площади пирамиды равна 54 + 72 + 6√181 = 126 + 6√181 см².
Объём пирамиды равен (1/3)*54*8 = 144 см³.
Ці точки лежать на серединному перпендикулярі точок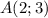 
та 
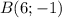. Знайдемо координати точки 
— середини відрізка 
:
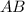Щоб знайти кутовий коефицієнт серединного перпендикуляра, знайдемо кутовий коефіцієнт прямої :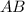
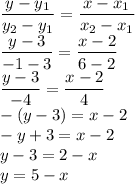
Коефіцієнт перпендикулярної прямої дорівнює 
. Застосуємо формулу прямої за кутовим коефицієнтом і точкою, через яку пряма проходить:
Тобто серединний перпендикуляр має формулу 
.
Знайдемо точку його перетину:
а) З віссю абсцисс:
Тобто точка має координати (3; 0).
б) З віссю ординат:
Все зобразив на графіку. Перемалюйте його в зошит, щоб отримати вищу оцінку ;)
Відповідь:
а) (3; 0)
б) (0; –3)
