ширина проёма ключа=25√3+1≈44,25мм
Объяснение:
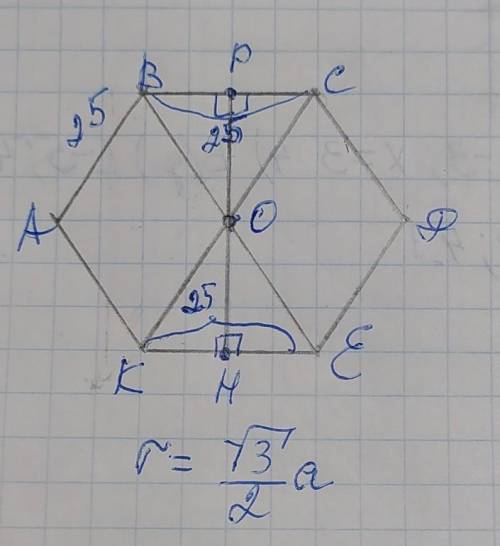
Проведём диагонали СК и ВЕ и обозначим точку их пересечения О, которая также является центром вписанной окружности. Проведём 2 радиуса ОР и ОН. Радиус вписанной окружности в правильном шестиграннике вычисляется по формуле:
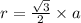
где а - любая сторона шестигранника.
Подставим в эту формулу наши данные:
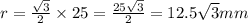
Ширина проёма ключа - это диаметр шестигранника РН+2×0,5мм зазора.
Поскольку диаметр - это 2 радиуса, то
РН=12,5√3×2=25√3мм
Зазор - это продолжение диаметра на 0,5мм от каждой из двух сторон шестигранника, поэтому зазор с двух сторон составит:
2×0,5мм=1мм
Тогда ширина проёма ключа равна 25√3+1
Можно так и оставить, но если нужно вычислить полностью, тогда √3≈1,73, и подставим это значение вместо корня:
25×1,73+1=43,25+1=44,25мм
Бесконечно много.
Объяснение:
Предположим, что таких сфер конечное количество. Выберем сферу с самым большим радиусом R. Пусть расстояние от центра сферы до плоскости окружности равно d. Тогда расстояние от центра этой сферы до любой из точек окружности равно R=√(r²+d²)
Восстановим перпендикуляр OH к плоскости окружности из ее центра O так, что OH=d1>d. Тогда расстояние от H до любой точки окружности равно R1=√(d1²+r²). Построим сферу с центром в H и радиусом R1. Из наших расчетов эта сфера будет проходить через исходную окружность. Осталось заметить, что R1=√(d1²+r²)>√(d²+r²)=R по построению, т.е. мы построили сферу, проходящую через данную окружность, с радиусом, большим R, несмотря на то, что по предположению это была сфера с самым большим радиусом, и при этом проходящая через данную окружность. Значит наше предположение неверно и таких сфер бесконечное количество.
Нехай вертикальні кути х°
їх сума х+х=2х°
Суміжний кут 180°-х°
складемо рівняння
2х-(180-х)=60
2х-180+х=60
3х=60+180
3х=240
х=80° - вертикальні кути
сума двох вертикальних кутів 80°+80°=160°
Суміжний кут 180°-80°=100°
Відповідь: кути 80°, 80°, 100°, 100°