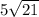Не знаю, как здесь обозначить вектор. Пусть будет ⁻. То есть, а⁻ - вектор а.
a⁻ (-5; -10); b⁻ (2; 7).
1) a⁻ + b⁻ (-3; -3)
2) 4 · a⁻ (-20; -40)
3) -2 · a⁻ + 3 · b⁻ (16; 41)
4) -b⁻ (-2; -7)
p⁻ (-3; 4); l⁻ (1; 2)
1) p⁻ - l⁻ (-4; 2)
2) Признак коллинеарности векторов: векторы коллинеарны, когда их координаты пропорциональны. Проверяем, вектор (p⁻ - l⁻) имеет координаты (-4; 2), а вектор k - координаты (4; -2).
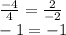
Так как их координаты пропорциональны, то эти векторы коллинеарны.
Если А (-2; 2), B (3; 5), то AB⁻ (5; 3).
Объяснение:
Задача № 1.
Дано: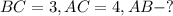
Решение: Так как ABC - прямоугольный треугольник, то AB можно найти по теореме Пифагора:
ответ: 5.
Задача № 2.
Дано: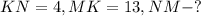
Решение: Так как NMK - прямоугольный треугольник, то NK можно найти по теореме Пифагора:
ответ: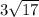
Задача № 3.
Дано: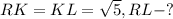
Решение: так как RKL - прямоугольный треугольник, то RL найдем через теорему Пифагора:
ответ: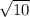
Задача № 4.
Дано: ∠M = 30°,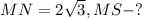
Решение: MNS - прямоугольный треугольник:
1. Так как катет NS лежит напротив 30 градусов, то он равен половине гипотенузы:
2. Найдем катет MS через теорему Пифагора:
ответ: 3
Задача № 5.
Дано: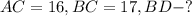
Решение: Рассмотрим треугольник BDC - прямоугольный:
BD найдем по теореме Пифагора:
ответ: 15
Задача № 6.
Дано: ΔRMN - правильный,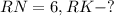
Решение: Рассмотрим ΔRKN - прямоугольный:
1. Высота делит основание пополам в правильном треугольнике:
2. Найдем высоту по теореме Пифагора:
ответ: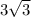
Задача № 7.
Дано: ΔMPR - правильный,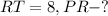
Решение: Рассмотрим ΔPTR - прямоугольный:
1. Высота делит основание пополам, тогда:
2. Найдем PR через теорему Пифагора:
Отрицательный корень нам не подходит, так как длина отрезка не может быть отрицательной.
ответ: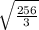
Задание № 8.
Дано: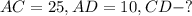
Решение: Рассмотрим ΔACD - прямоугольный:
Найдем CD по теореме Пифагора:
ответ: