Объяснение:
Теорема — сумма смежных углов всегда равна 180°
Углы — 1 = x; 2 = 2x; 3 = 3x; 4 = 90°
1) Составим уравнение и решим его:
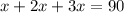
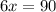
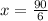
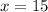
1 = 15°
2) Найдем остальные углы:
2 = 15°*2 = 30°
3 = 15°*3 = 45°
∠ALB = 120°.
Объяснение:
Дано: BL - медиана, BH⊥AC,BH - высота ,∠ACB = 60°, AC = 16, HC = 4
Найти: ∠ALB - ?
Решение: Так как BL - медиана по условию, то AL = LC = AC : 2 = 16 : 2 = 8.
LC = LH + HC ⇒ LH = LC - HC = 8 - 4 = 4.Треугольник ΔLHB = ΔCHB по первому признаку равенства треугольников так как, LH = HC = 4см, ∠LHB = ∠CHB = 90° так как по условию BH - высота, а сторона BH - общая для треугольников. Так как треугольник ΔLHB = ΔCHB, то соответствующие элементы треугольников равны, тогда ∠ACB = ∠BLC и ∠BLC = 60°.
Угол ∠ALB и ∠BLC - смежные, по свойству смежных углов их сумма 180°, тогда ∠ALB + ∠BLC = 180° ⇒ ∠ALB = 180° - ∠BLC = 180° - 60° = 120°.
Углы при основании равны, то есть если основание АС, то угол А = углу С.
Так как сумма углов любого треугольника равна 180 гр, то сумма углов А+С = 180-112=68 гр. Угол А=углу С = 68:2=34 гр.
Так как АF- биссектриса, то угол ВАF= углу САF= 34:2=17 гр.
Рассмотрим треуг. АВF, угол В=112 гр, угол ВАF=17 гр., тогда угол ВFА= 180 -112-17=51 гр.
Рассмотрим треуг АНF, угол АНF=90 гр, угол АFН=51 гр, тогда по свойству прямоугольного треугольника НАF= 90-51= 39 гр.
ответ F=51 гр, А=39 гр, Н=90 гр.
3x+2x+x=90 градусов.
6x=90 градусов.
x=15 градусов.
3x=3*15=45 градусов.
2x=2*15=30 градусов.
Объяснение: