S=16см²
Объяснение:
S=8²*sin2*45°/4=64*sin90°/4=64/4=16см²
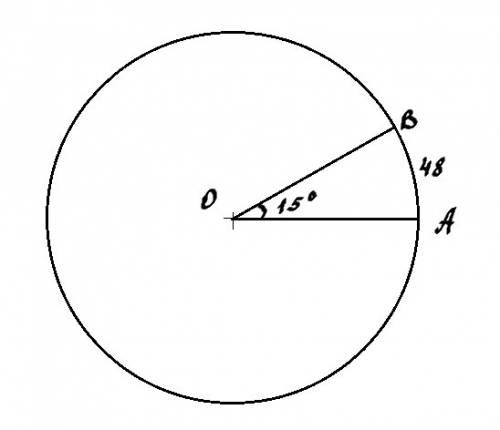
Угол АОВ центральный (смотри рисунок). Его градусная мера равна градусной мере дуги, на которую он опирается.
Малая дуга АВ равна 15°. Длина же ее равна 48.
Решим задачу, используя отношение.
Во сколько раз градусная мера большой дуги АВ больше градусной меры малой дуги АВ, во столько же раз длина большой дуги АВ больше длины малой дуги АВ.
Градусная мера всей окружности 360°.
360°–15° = 345° – градусная мера большой дуги АВ.
345°:15° = 23.
В 23 раза градусная мера большой дуги АВ больше градусной меры малой дуги АВ.
48*23 = 1104 – длина большой дуги АВ.
ответ: 1104.
Так как один острый угол = 45° , то и второй острый угол прямоугольного треугольника равен 90°-45°=45° .
Если два угла равны, то треугольник равнобедренный. Пусть оба катета равны а, тогда
а²+а²=8² , 2а²=64 , а²=32 , а=√32 .
Площадь треугольника равна S=1/2*a*a=1/2*a²=1/2*32=16 .