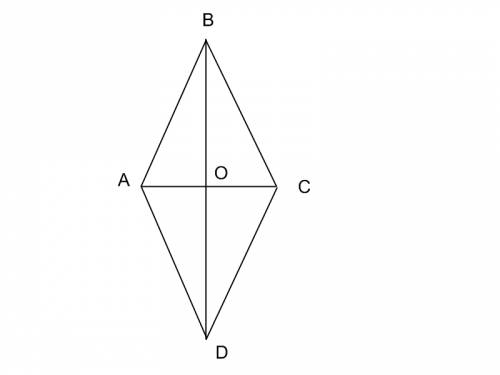
Дано: ABCD - ромб, BD=24см, AC=10см;
Найти: <A, <B, <C, <D;
Решение.
1) AB=BC=CD=AD, ВО=½BD, BO=12 и AO=½AC AO=5(по свойствам ромба), по теореме Пифагора AB²=BO²+AO², АВ²=12²+5², AB²=169, AB=13;
2)<A=<B=<C=<D, <ABO=<CBO, <BAO=<DAO(по свойствам ромба), sin ABO = AO/AB,
sin = 5/13, sin ABO≈0.38 <ABO≈68°, <BAO=180°-<BOA-<ABO, <BAO=180°-90°-68°=22°,
3) <A=44°, <B=136°, <C=44°, <D=136°
ответ: <A=44°, <B=136°, <C=44°, <D=136°.
площадь треугольника можно найти через полупериметр.
полупериметр = (10+17+21)/2=24
площадь: корень из (24*(24-10)*(24-17)*(24-21) = корень из 24*14*7*3 = корень из 7056
площадь = 84
радиус,описанной около треугольника, окружности = а*б*с/4S
10*17*21 / 4*84 = 85/8 = 10.625
радиус, вписанной в треугольник, окружности : площадь : полупериметр.
84/24= 3,5