1.danced, opened, took , rained, had , washed, did ,watched ,cleaned ,went, made , was , got ,lived , wrote
2.we didn't go to Moscow last summer.
the children didn't have dinner at 2o'clock yesterday.
they didn't watch film last week/
I didn't get up at 8 o'clock yesterday.
it didn't rain two days ago
Ann didn't live in S.Petersburg last year/
She didn't read an untersting book the day before yesterday.
I didn't my homework after school yesterday.
3.where the children play in the garden yesterday?
did Tom write a latter three days ago&
What father cook dinneh yesterday&
Who mother go to work by bus yesterday?
When we have a bath the day before yesterday?
Why Nick come home in the aafternoon?
What grandmother make tea in the morning?
4.1 We didn't have lunch at 1o'clock yesterday.Did we have lunch at 1o'clock yesterday? where we have lunch at 1 o'clock yesterday? Who have lunch at 1 o'clock yesterday?
4.2 It didn't show last week.Did it show last week? Where it show last week? Who ishow last week?
5/1 I halped the mom yesterday.
5/2 where you live last month?
5/3 Did they wake up at 7 am ?
5/4 We didn't go to school yesterday
5/5Who watch the TV on Sunday ?
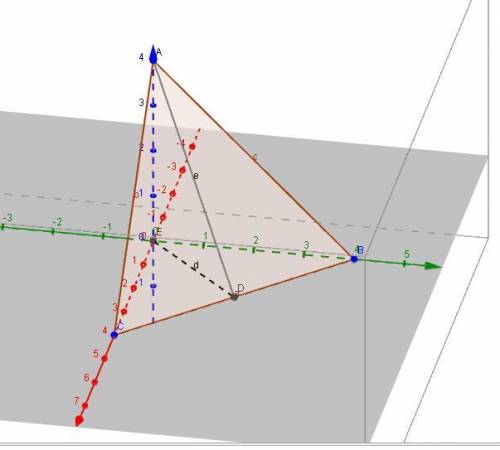
Эту задачу можно решить двумя .
1) Геометрический.
Так как плоскость отсекает на осях равные отрезки, то углы между осями и плоскостью равны.
Для примера возьмём угол к оси Oz.
Угол между прямой и плоскостью равен плоскому углу между этой прямой и её проекцией на плоскость.
Проекция оси Oz на плоскость лежит на прямой АД.
ОД = 4*cos 45 = 4*(√2/2) = 2√2.
Угол α = arc tg (2√2/4) = arc tg(√2/2) = 35,264 градуса.
2) Векторный.
Уравнение плоскости "в отрезках" (x/4) + (y/4) + (z/4) = 1.
В общем виде x + y + z - 4 = 0.
Направляющий вектор плоскости N = (1; 1; 1), его модуль равен √3.
Косинус угла между направляющим вектором плоскости и осью Oz равен: cos β = 1/√3. Сам угол равен arc cos(1/√3) = 54,7356 градуса.
Угол между нормалью к плоскости (прямой ее содержащей) и осями в сумме с искомым углом дают 90 градусов.
Тогда α = 90 - β = 90 - 54,7356 = 35,2644 градуса.
В равнобедренном треугольнике ABC высота BM является медианой.
AM=CM
△AMD=△CMD (по двум катетам, MD - общий)
AD=CD