α⊥β, α∩β = а.
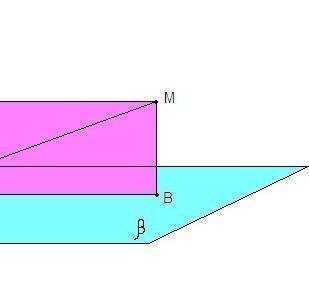
Проведем МА⊥α и МВ⊥β.
Тогда МА = 12 см - расстояние от точки М до плоскости α,
МВ = 5 см - расстояние от точки М до плоскости β.
Затем проведем АС⊥а и ВС⊥а.
Если прямая, лежащая в одной плоскости, перпендикулярна линии пересечения перпендикулярных плоскостей, то он перпендикулярна другой плоскости. Значит
АС⊥β и ВС⊥α.
АС║МВ и ВС║МА как перпендикуляры к одной плоскости, значит
МАСВ прямоугольник.
Прямая а перпендикулярна плоскости МАВ (а⊥АС и а⊥ВС), значит
а⊥МС.
МС - искомое расстояние от точки М до прямой а.
Из прямоугольного треугольника МАС по теореме Пифагора:
МС = √(МА² + АС²) = √(144 + 25) = √169 = 13 см
треугольники равны по второму признаку равенства треугольников.
(проводим прямую BD)
наложим ∆ABC на ∆ADC, так что бы вершина A совместилась с вершиной A1, B с B1, а D с D1 оказалась по разные стороны прямой A1 и C1.
треугольники равны по второму признаку равенства треугольников.