Рассомотрим треугольник СДЕ, так как он равнобедреный, то угол ДСЕ =углу ДЕС, значит эти углы =(180-уголД):2=(180-54):2=63градуса.
Рассотрим треугольник СЕF-прямоугольный, значит угол ЕСF=180- угол СFЕ - угол СЕF= 180-90-63 = 27градусов.
ответ: 27градусов
х - ширина площадки
(х + 10) - длина площадки , по условию задачи имеем : х *(х +10) = 9000
x^2 + 10x = 9000
x^2 + 10x - 9000 =0 . Найдем дискриминант квадратного уравнения - D
D = 10^2 - 4*1*(-9000) = 100 + 36000 = 36100 . Корень квадратный из дискриминанта равен 190 . Найдем корени квадратного уравнения : 1-ый = (- 10 + 190)/2*1 =180/2 = 90 ; 2-ой = (-10 - 190)/2*1 = -200/2 = - 100 . Второй корень не подходит так как х - это ширина площадки , а она не может быть меньше 0 . Значит ширина площадки равна 90 м. Отсюда длина площадки равна : х + 10 = 90 + 10 = 100 м
Объяснение:
остроугольный и равнобедренный.
Объяснение:
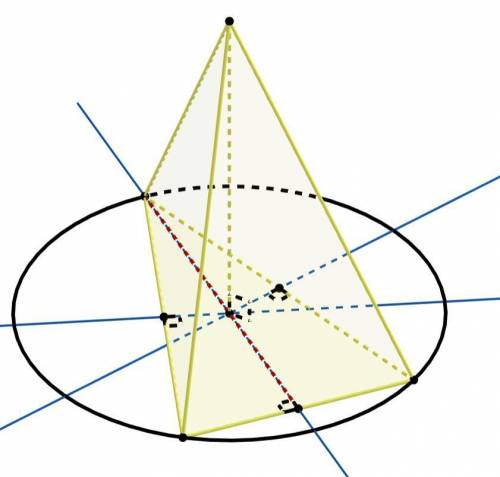
Если боковые рёбра пирамиды составляют равные углы с плоскостью основания, то основанием высоты пирамиды является центр окружности описанной около многоугольника из основания.
Центр окружности описанной около треугольника лежит внутри треугольника, если он остроугольный.
Так же этот центр лежит на пересечении серединных перпендикуляров к сторонам треугольника. Если центр описанной окружности лежит на одной высоте треугольника, то эта высота лежит на серединном перпендикуляре. А значит высота одновременно является и медианой. Тогда треугольник равнобедренный.
опустив высоту CF получается угол равный 90 градусов CFE. у равнобедренного треугольника углы при основании равны. 180 - 54 = 126 это сумма двух углов основания трегуольника. 126/2 = 63 градуса каждый угол, в данном случае нам нужен CEF. CFE = 90, CEF = 63. ECF= 180 - 90 + 63. получается 27 градусов. угол ECF = 27 градусов