Диагонали квадрата равны. Квадрат - это ромб, а площадь ромба равна половине произведения его диагоналей. Можно применить формулу площади ромба для нахождения площади квадрата:
S = (дм²)
Диагональ квадрата образует с двумя его сторонами прямоугольный треугольник, причем диагональ при этом является гипотенузой этого треугольника.
Пусть сторона квадрата x дм, тогда по теореме Пифагора:
Проведем вторую диагональ квадрата ВD, точку пересечения диагоналей обозначим О. Диагонали квадрата равны, пересекаются под прямым углом и точкой пересечения делятся пополам. Т.к. АМ=NC, то МО=NO. В четырехугольнике ВNDM диагонали перпендикулярны и точкой пересечения делятся пополам. Они делят его на 4 прямоугольных треугольника, в которых катеты равны, следовательно, эти треугольники равны, равны их гипотенузы и острые углы, т.е. диагонали - биссектрисы углов четырехугольника MBND. Т.к. накрестлежащие углы при пересечении сторон этого четырехугольника диагоналями ( биссектрисами) равны, то стороны BNDМ - параллельны, ⇒ BNDМ– параллелограмм. В параллелограмме ВNDМ стороны равны, его диагонали взаимно перпендикулярны, делят углы пополам, – это признаки ромба. ⇒ ВNDМ - ромб, ч.т.д.
32дм²
Объяснение:
Диагонали квадрата равны. Квадрат - это ромб, а площадь ромба равна половине произведения его диагоналей. Можно применить формулу площади ромба для нахождения площади квадрата:
S =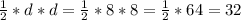 (дм²)
(дм²)
Диагональ квадрата образует с двумя его сторонами прямоугольный треугольник, причем диагональ при этом является гипотенузой этого треугольника.
Пусть сторона квадрата x дм, тогда по теореме Пифагора:
x² + x² = 8²
2x² = 64
x² = 32
x = √32 = √16*2 = 4√2 (дм)
Площадь квадрата x², то есть площадь равна 32дм²