Т.к. АС гипотенуза, становится ясно, что высота проведена из прямогу угла. А у такой высоты есть свойство, она равна среднему геометрическому отрезков нв которые она делит сторону к которой проведена. Т.е. в нашем случае АС^2=AD^2*DC^2. Найдем отсюда АC. DА=корень из(24^2-18^2)=корень из(252)
Теперь для начала найдем cosA. cosA=sinC(cвойство для прямоугольного треугольника)
а sinC в свою очередь равен24/BC. BC най дем по теореме пифагора из треугольника BDC. BC= корень из (24^2+18^2)=30 cosA=0,8
найдем АВ. Найдем по теореме Пифагора из треуг АВD. АВ=корень из(24^2+252)=
корень из(828)
----Картинка во вложении----
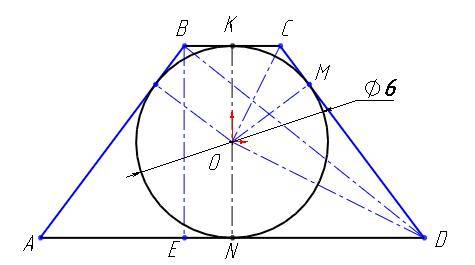
Рассмотрим равнобедренную трапецию ABCD со вписанной окружностью радиусом 3.
По условию сторона ВС равна половине высоты. Высота трапеции равна диаметру вписанной окружности, тогда
ВС=0,5*h=0,5*(3+3)=3
Найдем большее основание трапеции.
Рассмотрим два треугольника ОКС и OND. Они подобны. Тогда составим соотношение длин сторон
ОК/КС=ND/ON
То есть
3/1,5= ND/3
ND=3*3/1,5=6
AD=2*ND=2*6=12
Найдем площадь трапеции
S=KN*(BC+AD)/2=6*( 12+3)/2=45
Найдем длину диагонали.
Для этого рассмотрим треугольник DEB. Гипотенуза ВD этого треугольника является диагональю трапеции
Катет ВЕ = 6. Катет ЕD = ВС+(АD-ВС)/2=3+(12-3)/2=7,5
По длине катетов найдем длину гипотенузы
ВD=Корень квадратный из( ВЕ* ВЕ + ЕD* ЕD )= Корень квадратный из(6*6+7,5*7,5)=9,6
объяснение:
отдаленно похож на знак принадлежности