Правильная треугольная призма ABCA₁B₁C₁ ⇒ в основании лежит равносторонний треугольник, а боковые ребра перпендикулярны основаниям.
Прямые ВС и А₁С₁ - скрещивающиеся. Расстояние между скрещивающимися прямыми измеряется по их общему перпендикуляру. Так как ВС⊥СС₁ и А₁С₁⊥СС₁ ⇒ СС₁=16 см ⇒
АА₁=ВВ₁=СС₁= 16 см
ВК : КВ₁ = 3:5 ⇒ 3x+5x=16 ⇒ x=2
BK = 6 см; KB₁ = 10 см
Проведём BM⊥AC. BM - высота и медиана равностороннего ΔАВС. AM = MC
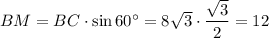 см
см
ΔABK=ΔCBK - равны по по двум катетам ⇒ AK=KC ⇒
ΔAKC - равнобедренный, AM=MC ⇒ KM⊥AC
KM⊥AC и BM⊥AC ⇒ ∠KMB - линейный угол двугранного угла между плоскостями ABC и AKC.
ΔKMB - прямоугольный, ВK = 6 см, ВМ = 12 см
tg ∠KMB = KB/BM = 6/12 = 0,5
ответ: 0,5
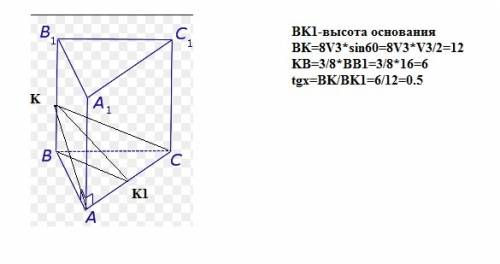
Правильная треугольная призма ABCA₁B₁C₁ ⇒ в основании лежит равносторонний треугольник, а боковые ребра перпендикулярны основаниям.
Прямые ВС и А₁С₁ - скрещивающиеся. Расстояние между скрещивающимися прямыми измеряется по их общему перпендикуляру. Так как ВС⊥СС₁ и А₁С₁⊥СС₁ ⇒ СС₁=16 см ⇒
АА₁=ВВ₁=СС₁= 16 см
ВК : КВ₁ = 3:5 ⇒ 3x+5x=16 ⇒ x=2
BK = 6 см; KB₁ = 10 см
Проведём BM⊥AC. BM - высота и медиана равностороннего ΔАВС. AM = MC
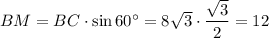 см
см
ΔABK=ΔCBK - равны по по двум катетам ⇒ AK=KC ⇒
ΔAKC - равнобедренный, AM=MC ⇒ KM⊥AC
KM⊥AC и BM⊥AC ⇒ ∠KMB - линейный угол двугранного угла между плоскостями ABC и AKC.
ΔKMB - прямоугольный, ВK = 6 см, ВМ = 12 см
tg ∠KMB = KB/BM = 6/12 = 0,5
ответ: 0,5

12 и 6
Объяснение:
Зная среднюю линию, можно найти сумму оснований:
9×2=18-сумма оснований.
теперь составим уравнение:
x+x+6=18
2x=12
x=6-меньшее основание
6+6=12-большее основание