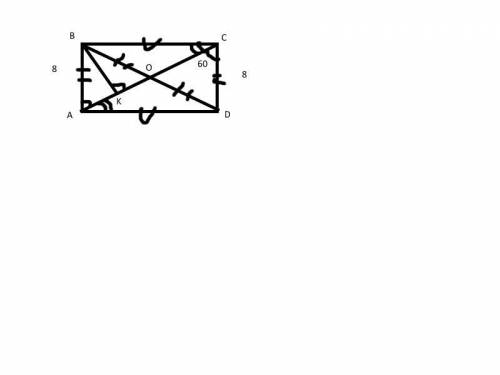
Дано: ABCD - прямоугольник
BK⊥AC
∠ACD=60°
AB=8 см
Найти: BD = ?
OK = ?
Т.к ABCD - прямоугольник, то AB=CD=8 см
∠OCD=∠BAO (н/л BC || AD и сек. AC) = 60°
∠BCO=∠OAD (н/л) = 90-60=30°
В прямоугольном ΔABC, ∠B=90°, ∠ACB=30°. Напротив угла в 30° в прямоугольном Δ лежит катет, равный половине гипотенузы => AB=0,5*AC => 8=0,5*AC => AC=8:0,5 => AC=16
Диагонали в прямоугольнике точкой пересечения делятся пополам => AO=OC=8 см.
ΔOCD - р/б т.к OC=CD => ∠COD=∠ODC. Сумма углов в треугольнике равна 180° => ∠COD=∠ODC= (180°-60°)/2=60° => ΔOCD - равносторонний по признаку => OD=OC=CD=8 см
BO=OD (диагональ делится пополам точкой пересечения)
BD=2*OD
BD=2*8
BD=16 см
ΔBOA - равносторонний (AB=BO=AO=8 см) => BK - высота, биссектриса и медиана => OK= 0,5*AO; OK=0,5*8; OK=4
ответ: BD = 16 см; OK = 4 см
Объяснение:
1)т.к Δ АВС - прямоугольный 1) можно найти АВ по т. Пифагора:
АВ - гипотенуза АВ²=9+16=25
АС=3 см ⇒ АВ=5 см
СВ=4 см
угол С- прямой =90⁰
найти: АН-?
НВ-?
Высота СН -?
2)из св-ва прямоугольного треугольника( высота, опущенная из вершины прямого угла на гипотенузу, делит его на 2-а подобных Δ-ка, каждый из которых подобен данному тр-ку) т.е ΔАСН подобен ΔСВН СВ²=АВ*НВ (1)
ΔАСН подобен ΔАВС ⇒ АС²=АВ*АН (2) ⇒
ΔСВН подобен ΔАВС СН²=АН*ВН (3)
⇒ теперь подставляем (СВ=4, АВ=5) в (1)получаем 16=5*НВ
НВ=16/5=3,2
теперь подставляем во (2) (АС=3, АВ=5) получаем 9=5*АН
АН=9/5=1,8
и в (3) подставляем то что нашли и получаем: СН²= 1,8*3,2
СН=√5,76=2,4
ответ:АН=1,8 см; НВ=3,2 см; СН=2,4 см
1) Обозначим неизвестную сторону х.
cos150°= -cos30°= -√3/2
По т.косинусов:
х²=(4√3)²+7² - 2•4√3•7•(-√3/2)
x²=48+49+84
x=√181 см