А₁В₁С₁Д₁ -ромб, площадь которого равна А₁С₁*В₁Д₁/2=6*12/2=36/cм²/. Зная половины диагоналей 6/2 и 12/2, можно найти сторону, т.к. диагонали пересекаются под прямым углом. значит. сторона равна √(3²+6²)=
√(9+36)=3√5, ∠СВ₁С₁=30°. т.к. В₁С₁- проекция В₁С на плоскость основания. Тогда высота призмы СС₁=В₁С₁**tg30°=
3√5*(1/√3)=√15
Объем равен произведению площади на высоту. т.е. 36*√15=/см³/
Площадь полной поверхности состоит из двух площадей основания, т.е. 2*36=72, и боковой поверхности 4*В₁С₁*СС₁=4*(3√5)*(√15)=60√3
=4*3*3*5√3=90√3
площадь полной поверхности равна (72+60√3) см²
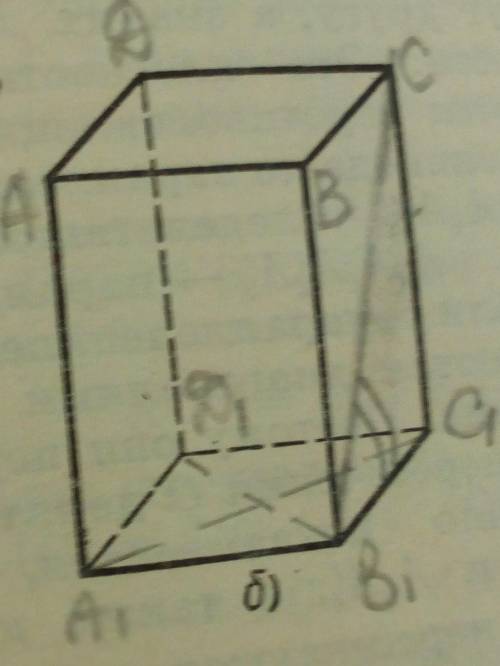
а) CosCBD = 0,96.
б) ВС = 5 ед.
Объяснение:
Треугольник CDE - прямоугольный, так как СЕ² = СD² + DE².
(25² = 24² + 7² или 625 = 576 +49 => 625=625). =>
СЕ - диаметр окружности.
а) Cos(∠CED) = ED/CE = 24/25 = 0,96.
∠CED = ∠CBD как вписанные, опирающиеся на одну дугу СD.
Значит CosCBD = 0,96.
б) По теореме синусов в треугольнике CBD имеем:
CD/SinB = BC/SinD. SinB = √(1-Cos²B) = √(1-0,96²) = 0,28. (косинус угла В нашли в пункте а). =>
ВС = CD·SinD/SinB = 7·(1/5)·0,28 = 5 ед.