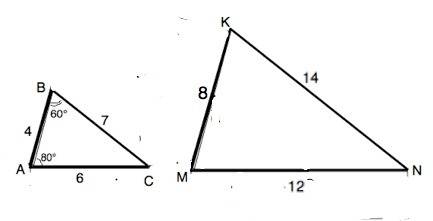
Объем усеченной пирамиды равен 1/3*H*(S₁+√(S₁S₂)+S₂), где H-высота, S₁-площадь 1 основания, S₂ - площадь 2-го основания, причем основания прям треугольники (Пусть будут О1, О2 соотвественно). S₁- площадь О1. S₁=1/2*6*8=24. Гипотенуза О1 равна √(6²+8²)=√100=10. Тогда Р(Периметер) О1 равна 6+8+10=24.
Т.к. 24=12*2, то Р(О2) =P(O1)/2 = > стороны O2 в 2 раза меньше сторон O1, т.е. катеты О2 равны 3 и 4 => S₂=3*4/2=6.
Тогда объем усеченной пирамиды равен 1/3*6*(24+√(6*24)+6)=2(24+12+6)=2*42=84 см³
найдем сторону основания а -- а=d/√2
тогда площадь граней АВК = КВС= 1/2*h*a=1/2*h*d/√2
найдем длину ребер АК=КС=c=√(h^2+a^2)=√(h^2+(d/√2)^2)
тогда площадь граней АDК = КDС=1/2*ca=1/2*√(h^2+(d/√2)^2)*d/√2
Sбок=S(АВК)+S(КВС)+S(АDК)+S(КDС)=2*1/2*h*d/√2 +2*1/2*√(h^2+(d/√2)^2)*d/√2=
=h*d/√2 +√(h^2+(d/√2)^2)*d/√2=d/√2 *(h+√(h^2+(d/√2)^2))
подставим значения из условия