Треугольник АВС. Угол А : углу В : углу С = 1:3:5
х+3х+5х=180
9х=180
х=20
Угол А = 20 град
Угол В = 20*3=60 град
Угол С = 20*5=100 град
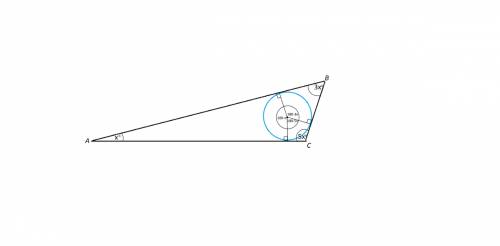
Р, М, К - точки касания окружности сторон треугольника соответственно на сторонах АВ, ВС и АС
О - центр окружности
Рассмотрим четырёхугольник АКОР. УголК + угол Р =90+90=180 град (радиусы, проведённые в точки касания), значит
угол КОР + уголА = 360-180=180 град
угол КОР = 180-20=160 град.
Аналогично рассуждаем при нахождении углов РОМ и МОК
угол РОМ = 180-60=120 град
угол МОК = 180-100=80 град
∠ВЕС = 34°.
Объяснение:
Треугольник АВС - равнобедренный. (АВ=ВС) => (∠BAC = ∠BCA).
Тогда ∠DAB = ∠ACF равны как смежные с равными углами.
Треугольники ABD и FCF равны по двум сторонам (AD=AC, AB=CF) и углу между ними (∠DAB = ∠ACF).
В равных треугольниках против равных сторон лежат равные углы. Следовательно, ∠DBA = ∠AFC = 31°, а ∠CAF = ∠BDA = 25°.
∠BCA - внешний угол треугольника АСF и равен сумме двух углов, не смежных с ним, то есть ∠BCA = ∠CAF + ∠CFA = 25+31 = 56°.
∠СВЕ - внешний угол треугольника АВС => ∠СВЕ = ∠BAC + ∠BCA.
∠СВЕ = 56+ 56 = 112°.
Треугольник СВЕ равнобедренный и ∠ВЕС = ∠ЕСВ = (180 - 112/2 = 34° по сумме углов треугольника.
ответ: ∠ВЕС = 34°.