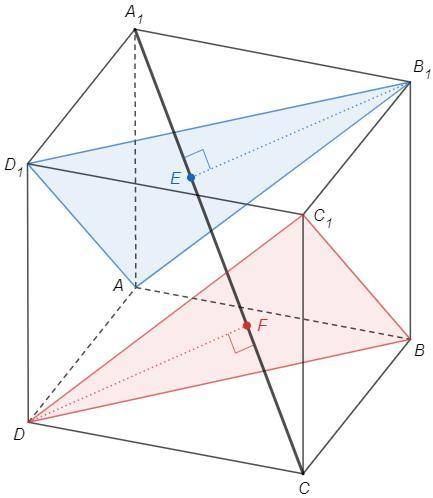
Диагонали противоположных граней куба параллельны.
AB1||DC1, D1B1||DB => (AB1D1)||(C1BD)
Достаточно найти расстояние между параллельными плоскостями.
A1AB1D1 и СAB1D1 - правильные пирамиды, вершины A1 и С проецируются в центр основания E.
То есть A1C⊥(AB1D1)
Аналогично A1C⊥(C1BD)
EF - искомое расстояние.
AB1 =√2 (диагональ квадрата)
B1E =√3/3 *AB1 =√6/3 (радиус описанной окружности правильного треугольника)
A1E =√(A1B1^2 -B1E^2) =√(1 -6/9) =√3/3
A1E =CF (высоты в равных пирамидах)
A1C =√3 (диагональ куба)
Таким образом EF =√3/3
Объем V = 1*7*8 = 56 кубических единиц. Каких неизвестно, не даны.
2) См. рисунок. Так как распилили на кубики с ребром 3 см, то таких кубиков на каждом ребре получилось по 6 штук. Понятно, что крайние кубики на каждом ребре будут иметь по три красных грани. А оставшиеся между ними четыре кубика будут иметь по две красных грани. Всего ребер 12. Значит всего кубиков с двумя красными гранями будет 4*12 = 48 штук.