1)
1. E
2. F
3. B
4. E
5. A
6. D.
Теорема косинусов: 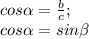
Теорема синусов: 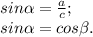
3)
Формула вычисления стороны, зная 2 другие, и угол между ними:
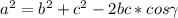
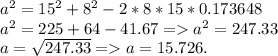
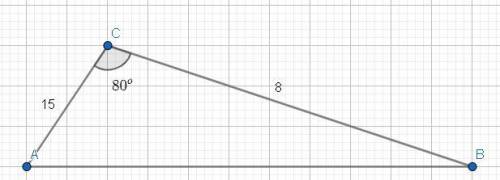
Так как путь из A => B проходит через пункт C, то в этом случае, расстояние между точками A & B равна: AC+BC = 23.
Но так как мы уже нашли 3-ю недостающую сторону(AB(в 1-ой картинке)), то расстояние между точками A => B, без прохода через точку C — равна 23-15,726 = 7.242.
4)
Формула вычисления описанной окружности около равнобёдренного треугольника такова: 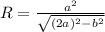
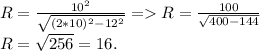
Формула вычисления вписанной окружности около равнобёдренного треугольника такова: 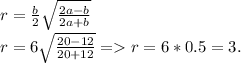
1. Синусы углов пропорциональны сторонам треугольника
Нет такой теоремы.
2. Cтороны треугольника пропорциональны косинусам противоположных им углов
Нет такой теоремы, но выражение присутствует. Это:
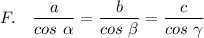
3. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними
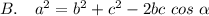
4. Стороны треугольника пропорциональны синусам противоположных им углов
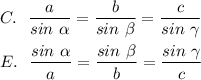
5. Квадрат стороны треугольника равен сумме квадратов двух сторон минус удвоенное произведение этих сторон на синус угла между ними
Нет такой теоремы, но выражение присутствует. Это:
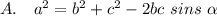
6. Квадрат стороны треугольника равен сумме квадратов двух других сторон плюс удвоенное произведение этих сторон на косинус угла между ними
Нет такой теоремы, но выражение присутствует. Это:
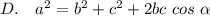
Теорема косинусов 3 (В)
Теорема синусов 4 (C и Е)
82
Объяснение:
На один угол ,например при верхнем основании, приходится 196:2=98.
Сумма всех углов четырехугольника равна 360.Значит на два остальных угла остается 360-196=164.На один угол, например при нижнем основании, приходится 164:2=82