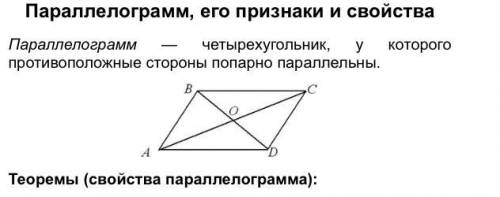
Теоремы (свойства параллелограмма):
В параллелограмме противоположные стороны равны и противоположные углы равны: AB = CD, BC = AD, \angle ABC = \angle
ADC,\angle BAD = \angle BCD.
Диагонали параллелограмма точкой пересечения делятся пополам: AO
= OC, OB = OD.
Углы, прилежащие к любой стороне, в сумме равны 180^\circ .
Диагонали параллелограмма делят его на два равных треугольника.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон: AC^2 + BD^2 = 2AB^2 + 2BC^2 .
Признаки параллелограмма:
Если противоположные стороны четырехугольника попарно параллельны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике диагонали, пересекаясь, точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Середины сторон произвольного (в том числе невыпуклого или пространственного) четырехугольника K,\;L,\;M,\;N являются вершинами параллелограмма Вариньона.
Треугольником называется фигура,состоящая из трех точек не лежащих на одной прямой и трех отрезков соединяющих эти точки.
Периметр треугольника- это сумма длин трех сторон треугольника.
(рисунок во вложении)
№2
Равными треугольниками называют такие треугольники у которых равных соответствующие элементы(стороны и углы)
№3
Теоремой называют утверждение,справедливость которого устанавливают путем рассуждений,а сами рассуждения называются докозательствами теоремы.
№4
Первый признак равенства треугольников
Если две стороны и угол между нимми одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника,то такие треугольники равны.
Доказательство стр 30.
№5
Отрезок АН называется перпендикуляром,проведенным из точки А к прямой а,если прямые АН и а перпендикулярны. Рисунок на стр 32(рис. 55)(рис. 55)
№6
Теорема
Из точки,не лежащей на прямой,можно провести перпендикуляр к этой прямой,и притом только один. (доказательство страница 32)
№7
Отрезок,соединяющий вершину треугольника с серединой противоположной стороны,называется медианой треугольника
Всего треугольник имеет 3 медианы
№8
отрезок,биссектрисы угла треугольника,соединяющий вершину треугольника с точкой противоположной стороны,называется биссектрисой треугольника.
Треугольник имеет три биссектрисы.
№9
Перпендикуляр,проведенный из вершины треугольника к прямой,содержащей противоположную сторону,называется высотой треугольника.
Любой треугольник имеет три высоты.
№10
Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми сторонами,а третья сторона называется основанием.
№11
Треугольник,все стороны которого равны называется равносторонним.
№ 12
Докозательство на странице 35
№13
Теорема
В равнобедренном треугольнике биссектриса проведенная к основанию является медианой и высотой(доказательсво стр 35-36)
№14
Если сторона и два прелижащей к ней угла одного треугольника соответственно равным стороне и двум прелижащим к ней углам другого треугольника,то такие треугольники равны.( доказательство на странице 38-39)
№15
Если три стороны олного треугольника соответственно равным трем сторонам другого треугольника,то такие треугольника равны. (доказательство 39-40 стр)
№16
Определение- предложение, в котором разъесняется смысл того или иного выражения или названия.
Окружность-геометрическая фигура состоящая из всех точек плоскости расположенных на заданном расстоянии от данной точки
Центр-данная точка.
радиус- отрезок соединяющий центр с какой-либо точкой окружности
хорда-отрезок соединяющий две точки окружности
диаметр-хорда проходящая через центр.
ответы на вопросы главы III
№1
Две прямые называются паралльными если они не пересекаются.
Два отрезка называются параллельными,если они лежат на параллельных прямых.
№2
Прямая с называется секущей по отношению к прямым а и в если она пересекает их в двух точках.образуются углы: накрестлежащие,односторонние и соотвественные.
№7 аксиома- исходные положения
примеры:
через любые две точки проходит прямая и притом только одна
на любом луче от его начала можно отложить отрезок равный данному и притом только один.
№9
через точку не лежащую на данной прямой проходит только одна прямая параллельная данной
№10
следствия- утверждения которое выводятся непосредственно из аксиом или теорем
№ 12
теорема обратной данной называется такая теорема в которой условием является заключение данной теоремы,а заключением-условие данной теоремы.
Пример: если две параллельные прямые пересечены секущей,то накрестлежащие углы равны.
ответы на вопросы для повторения к главе IV
№1
Сумма углов треугольника равна 180 градусам
№2
Внешний угол-угол смежный с каким-нибудь углом этого треугольника.
№4
остроугольным треугольником называют треугольник если все его углы острые
тупоугольным треугольником называют треугольник,если один из его углов тупой
№5
прямоугольным треугольником называют треугольник у которого один из его углов прямой.
Сторона лежащая против прямого угла называется гипотенузой, две другие-катетами.
№ 9
Неравенство треугольника выходит из следствия:
Для любых трех точек А,В,С не лежащих на одной прямой справедливы неравенства
АВ< АС+ВС, АС<АВ+ВС, ВС<ВА+АС.
Каждое из этих неравенств называется неравенством треугольника.
№12
Если гипотенуза и острый катет одного прямоугольного треугольника соответсвенно равны гипотенузе и острому углу другоого прямоугольного треугольника,то такие треугольники равны
№13
Если гипотенуза и катет одногоо прямоуголльного треугольника соответсвенно равны гипотенузе и катету другого то такие треугольники равны.
№ 16
Расстоянием от точки до прямой называется длина перпендикуляра проведенного из точки к прямой.
№ 18
Расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми.