1)
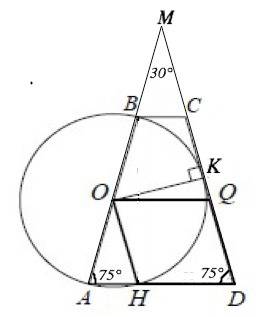
О- центр окружности ⇒ середина АВ, Q - середина СD.
ОQ соединяет середины боковых сторон трапеции ⇒
OQ как средняя линия трапеции параллельна АD.
Т.к. трапеция равнобедренная, АО=DQ
Углы при основании равнобедренной трапеции равны, АО=НО ( радиусы), треугольник АОН - равнобедренный,∠ОНА=∠ОАН и равен углу QDH. Соответственные углы при пересечении прямых ОН и QD секущей АD равны, следовательно. ОН||QD.
Противоположные стороны четырёхугольника DQOH попарно параллельны, следовательно, DQOH — параллелограмм.
2)
Продолжим боковые стороны трапеции до пересечения в т.М. Углы при основании равнобедренной трапеции равны. Следовательно,
угол АМD=180°-2•75°=30°
Проведем ОК в точку касания. Радиус, проведенный в точку касания, перпендикулярен касательной.
∠ МКО=90°
В прямоугольном ∆ МОК катет ОК противолежит углу 30°, ⇒
гипотенуза МО=2ОК. Т.к. ОК=ОВ=R, МО=2 R.
Тогда MA=3R .
BC║OQ║AD ⇒ ∆BMC~∆ AMD. k=AM:BM=3 ⇒
AD=3BC=3 (ед. длины)
R = 10см; R/h = 1/2
Объяснение:
Площадь полной поверхности цилиндра
S = 2πR² + 2πRh = 2πR(R + h) = 1884
Сокращаем на 2π = 6,28 и получаем R(R + h) =300
или R² + Rh = 300
Обозначим х = R и у = Rh
Тогда у = 300 - х²
При условии максимального объёма цилиндра
V = πR²h = π · R · Rh = π · x · y, то есть следует искать максимум функции
f(x) = x·у
f(x) = х · (300 - х²)
f(x) = 300x - x³
f'(x) = 300 - 3x²
f'(x) = 0
300 - 3x² = 0
x² = 100
x = 10(см)
Итак, R = 10см
y = Rh = 300 - 10² = 200
h = Rh/R = 200/10 = 20 (см)
Отношение R/h = 10/20 = 1/2
ответ во вложении.