Задача: Известно, что в треугольниках АВС и А1В1С1 А = А1, АВ = А1В1, АС = А1С1. На сторонах ВС и В1С1 отмечены точки К и К1, такие, что СК = С1К1. Докажите, что ∆ АВК = ∆ А1В1К1.
ответы:Δ АВС=ΔА1В1С1 по первому признаку равенства треугольников, так как ∠А=∠А1, АВ=А1В1,АС=А1С1- по условию.
В равных треугольниках соответственные стороны равны,
значит ВС=В1С1, тогда ВК=В1К1, так как КС=К1С1 - по условию.
В ΔАВК иΔА1В1К1:
АВ=А1В1, ВК=В1К1, ∠В=∠В1, значит ΔАВК =ΔА1В1К1 по первому признаку равенства треугольников, что и требовалось доказать.
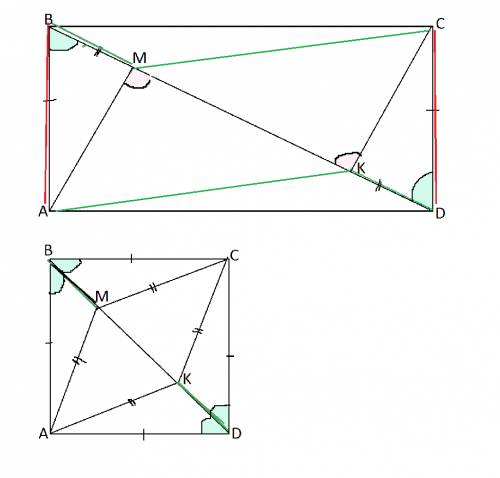
Рисунок: картинка
Рассмотрим два варианта:
1) Боковая сторона равна 16 дм. Этому же равна другая боковая сторона.
Тогда основание равно 60-16-16=28 дм
ответ: 16 дм; 16 дм; 28 дм.
2) Основание равно 16 дм.
Тогда каждая из боковых сторон равна (60-16)/2=22дм
ответ: 16дм; 22 дм; 22 дм.
Если будут вопросы – обращайтесь :)