108 см²
Объяснение:
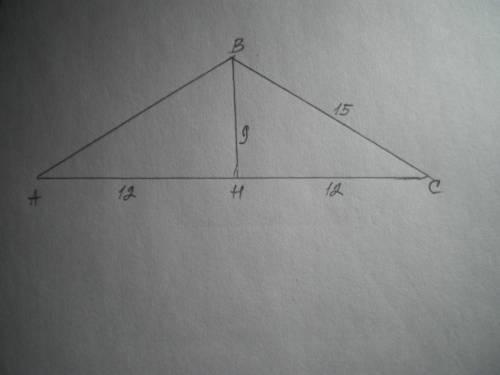
Дано: ΔАВС - равнобедренный, АВ=ВС=15 см, АС=24 см. Найти S(АВС).
Проведем ВН - высоту и медиану. Тогда АН=СН=24:2=12 см.
Рассмотрим ΔАВН - прямоугольный, АВ=15 см, АН=12 см, значит ВН=9 см (египетский треугольник).
S=1/2 * АН * ВН = 1/2 * 24 * 9 = 108 см²
1) В любом треугольнике центр вписанной окружности лежит внутри треугольника, так как биссектрисы треугольника пересекаются внутри треугольника.
2) В правильном треугольнике центры вписанной и описанной окружностей совпадают.
3) В остроугольном треугольнике центр описанной около него окружности лежит внутри треугольника.
4) В тупоугольном треугольнике центр описанной около него окружности лежит вне треугольника.
5) В прямоугольном треугольнике центр описанной около него окружности лежит в центре гипотенузы.
ответ: 30°.
Объяснение:
ΔОСВ: ОС=ОВ как радиусы одной окружности ⇒
ΔОСВ - равнобедренный, значит ∠ОВС=∠ОСВ=60° по свойству углов при основании равнобедренного треугольника.
Из теоремы о сумме углов треугольника:
∠СОВ=180°-(∠ОВС+∠ОСВ)=180°-(60°+60°)=60°.
ΔАОВ: АО=ВО как радиусы одной окружности ⇒
ΔАОВ - равнобедренный.
ОD- медиана ΔАОВ, т.к. АD=DВ по условию ⇒ ОD - биссектриса ⇒
∠ АОD=∠ВОD=60°, ∠ АОВ=∠АОD+∠ВОD=60°+60°=120°.
∠ ОАВ=∠ ОВА по свойству углов при основании равнобедренного треугольника.
Из теоремы о сумме углов треугольника:
∠ ОАВ=(180°-120°):2=60°:2=30°.
Решение на фото.
Стараюсь быть лучшим для вас!