ответ: 16см²
Объяснение: если при основании каждый угол составляет 45°, то этот треугольник прямоугольный, так как сумма углов треугольника составляет 180°- это легко проверить:
180–45–45=90°
Обозначим вершины треугольника А В С с прямым углом С катетами АС и ВС и гипотенузой АВ. Если основание=8, то оно буде являться гипотенузой и поэтому легко вычислить катеты с синуса или косинуса угла, поскольку значение и синуса и косинуса буде одинаковым при величине угла 45°
АС=ВС=АВ×sin45°=8×√2/2=4√2
Площадь прямоугольного треугольника вычисляется по формуле: S=AC×BC/2=
=4√2×4√2/2=16×2/2=16см²
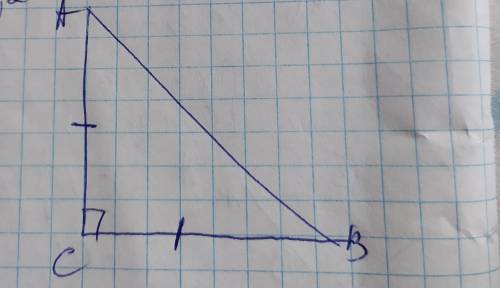
ответ: 192 см²
Объяснение:
У куба все грани квадраты. Диагонали квадрата равны и точкой пересечения делятся пополам.
Пусть О - точка пересечения диагоналей грани ABCD.
В треугольнике АВ₁С проведем отрезок ТО.
ТО - средняя линия треугольника АВ₁С, значит ТО ║ АВ₁,
т.е. ТО - это отрезок прямой k, проходящей через точку Т параллельно прямой АВ₁, расположенный внутри куба.
АВ₁ = 2ТО = 2 · 4 = 8 см по свойству средней линии.
Площадь квадрата можно найти как половину квадрата его диагонали (квадрат - ромб с равными диагоналями, а площадь ромба равна половине произведения его диагоналей):
Saa₁b₁b = 1/2 AB₁² = 1/2 · 64 = 32 см²
Площадь поверхности куба:
Sпов = 6 · Saa₁b₁b = 6 · 32 = 192 см²