11. <MAL=110° 12. АС=4см
Объяснение:
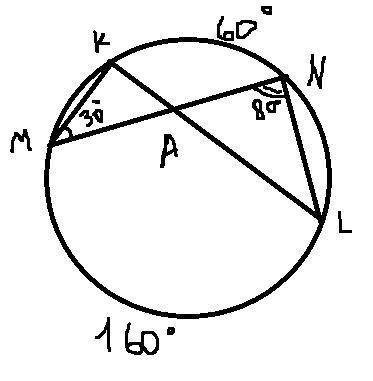
11. дуга KN = <KMN*2=60, дуга ML = <MNL*2=160
Угол между пересекающимися хордами равен полусумме противоположных дуг, высекаемых хордами.
<MAL=(KN+ML)/2=(60+160)/2=110°
рисунок к 11 задаче
12. Произведение длины секущей на ее внешнюю часть равно квадрату длины касательной.
AC - расстояние от С до пересечения секущей и окружности.
BC*AC=CD²
Пусть AC=x, тогда BC=12+x.
(12+х)х=64
х²+12х-64=0
D=144+4*64=400
x=(-12±√400)/2=-16;4
Берём только положительный корень уравнения - 4
Такой треугольник не существует, потому что две его стороны с меньшими длинами (20 см и 25 см) суммарно меньше, чем его большая сторона (50 см). То есть, даже если угол между меньшей и большей сторонами будет равен нулю (они совпадут, наложившись друг на друга), а угол между двумя меньшими сторонами будет равен 180 (это будет развернутый угол, то есть, они будут лежать на одной прямой), длины двух меньших сторон не хватит, чтобы вершина (последняя точка) суммы меньших сторон коснулась последней точки большей стороны.
Центральный угол в развёртке боковой поверхности конуса равен 120°. Высота конуса=4√2. Найдите его объем.
----------
Образующая конуса L- радиус окружности с центром В, частью которой является его развертка АВС.
Формула длины окружности =2πR =2πL, где L- образующая конуса.
Т.к. угол АВС=120°, а полная окружность содержит 360°, длина дуги АС=1/3 длины окружности, содержащей развертку конуса.
◡AC=2πL/3
В то же время дуга АС этой окружности равна длине окружности основания конуса.
2πr=2πL/3 ⇒ L=3r
Из треугольника, образованного высотой конуса и радиуса ( катеты) и образующей ( гипотенуза) найдем по т.Пифагора радиус основания конуса.
L²-r²=h²
9r²-r²=32
r²=32:8=4
V(кон)=πr²•h/3
V=(π4•4√2):3=(π16√2):3
V=\frac{pi4*4\sqrt{2}}{3}=\frac{16\pi\sqrt{2}}{3}V=
V=
3
= ответ объёма на картинке