Тема: "окружающая среда"
* * * для удобства плоскость (ABCD) обозначаем через Ψ * * *
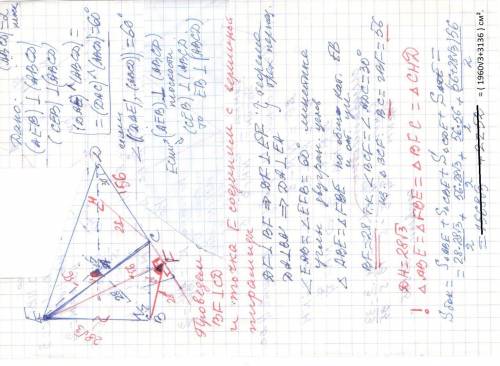
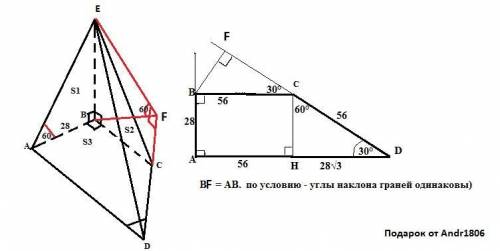
EABCD - пирамида , основание которой трапеция ABCD ;
AD || BC ; AB =28 ; ∠A =∠B =90° ; ∠D =30° ; | [AB] < [CD] ; [BC] < [AD]
(ABE) ⊥ Ψ и (CBE) ⊥ Ψ ; ∠ ( (CDE) , Ψ ) =∠ ( (ADE) , Ψ ) = 60°
--------------------------
1. Трапеция ABCD ПРЯМОУГОЛЬНАЯ
- - -
(ABE) ⊥ Ψ и (CBE) ⊥ Ψ ⇒ EB ⊥ Ψ
DA⊥ BA ⇒DA ⊥ EA ; ∠EAB =60° линейный угол двугранного угла
EADC ; Построим линейный угол двугранного угла EDCA
Проведем BF ⊥ CD и основание F этого перпендикуляра соединим с вершиной ПИРАМИДЫ E. Получаем ∠EFB = 60° линейный угол двугранного угла EDCA .
* * * ! ΔABE = ΔFBE =Δ BFC = ΔCHD учитывая ∠D =∠BCF =30° * * *
Вычисление площадей боковых граней и т.д. cм приложение
1.
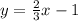
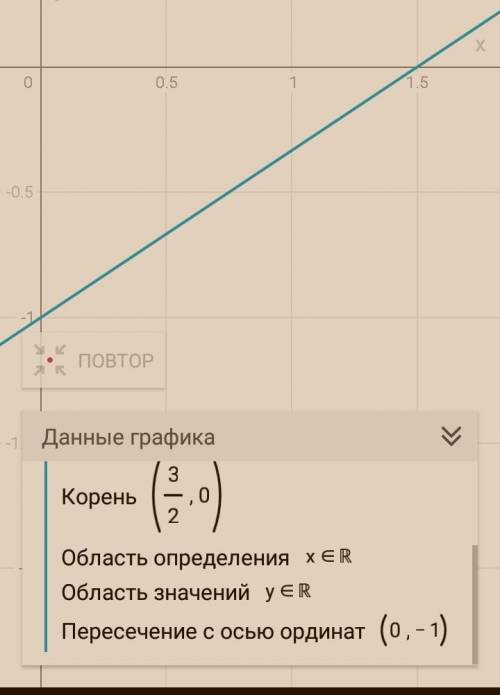
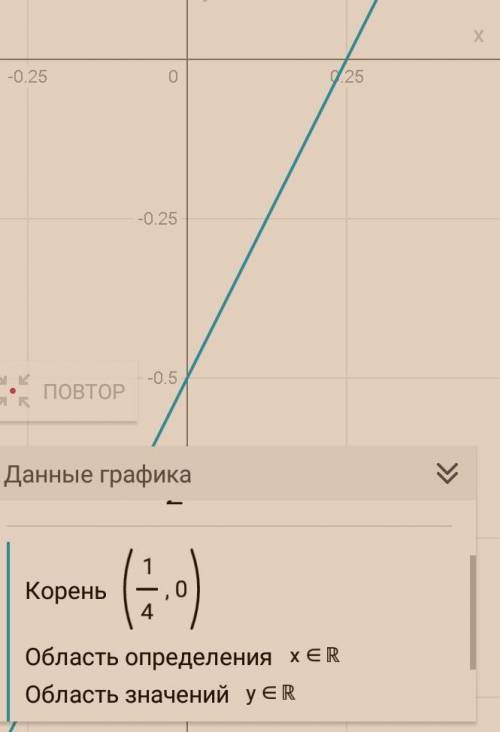
Первый вариант решения: найти пересечение с осью Х/корень
1) за место у=0
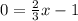
2) решить уравнение относительно Х
(сам сделаешь, я тебе только ответ пришлю)
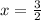
Альтернативные ответы:
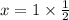

Второй вариант решения: найти пересечение с осью У
1) заменяем Х=0
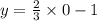
2) реши уравнение относительно У
(снова запишу конечный результат)
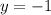
2.
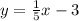
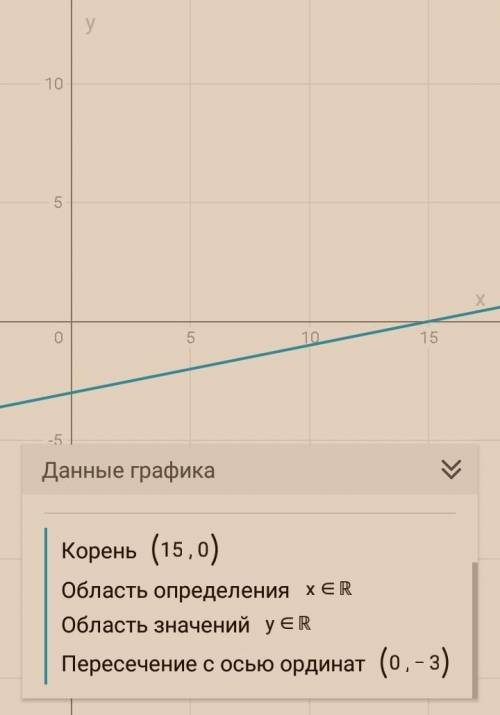
Первый вариант: через Х
1) заменяет У=0
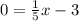
2) решаем уравнение
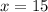
Второй вариант решения: через У
1) заменяем Х=0
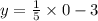
2) решить уравнение
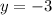
3.
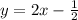
Первый вариант: через Х
1) заменяем У=0
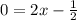
2) решить уравнение
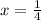
Альтернативная форма
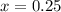
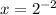
Второй вариант: через Х
1) заменяем Х=0
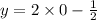
2) решить уравнение
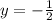
Альтернативный вариант
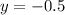
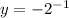

Дано :
Четырёхугольник ABCD - прямоугольник.
Отрезки АС и BD - диагонали.
Точка О - точка пересечения диагоналей.
∠CAD = 45°.
Найти :
∠AOD = ?
∠А = ∠В = ∠С = ∠D = 90° (по определению прямоугольника).
Тогда -
∠OAD + ∠BAO = 90°
∠BAO = 90° - ∠OAD = 90° - 45° = 45°.
Мы получаем, что - ∠BAO = ∠OAD (это значит, что отрезок АС не только диагональ, но и биссектриса ∠А, так как делит этот угол пополам).
Если в прямоугольнике диагональ является также его биссектрисой, то этот прямоугольник - квадрат.Диагонали квадрата взаимно перпендикулярны.Тогда получаем, что -
∠AOD = 90°.
90°.