1)
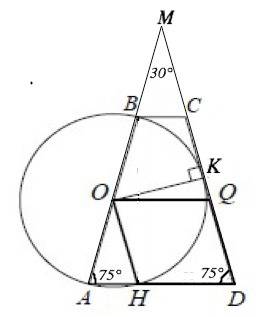
О- центр окружности ⇒ середина АВ, Q - середина СD.
ОQ соединяет середины боковых сторон трапеции ⇒
OQ как средняя линия трапеции параллельна АD.
Т.к. трапеция равнобедренная, АО=DQ
Углы при основании равнобедренной трапеции равны, АО=НО ( радиусы), треугольник АОН - равнобедренный,∠ОНА=∠ОАН и равен углу QDH. Соответственные углы при пересечении прямых ОН и QD секущей АD равны, следовательно. ОН||QD.
Противоположные стороны четырёхугольника DQOH попарно параллельны, следовательно, DQOH — параллелограмм.
2)
Продолжим боковые стороны трапеции до пересечения в т.М. Углы при основании равнобедренной трапеции равны. Следовательно,
угол АМD=180°-2•75°=30°
Проведем ОК в точку касания. Радиус, проведенный в точку касания, перпендикулярен касательной.
∠ МКО=90°
В прямоугольном ∆ МОК катет ОК противолежит углу 30°, ⇒
гипотенуза МО=2ОК. Т.к. ОК=ОВ=R, МО=2 R.
Тогда MA=3R .
BC║OQ║AD ⇒ ∆BMC~∆ AMD. k=AM:BM=3 ⇒
AD=3BC=3 (ед. длины)
Катет а = 6; гипотенуза с = 100
Найдём второй катет по теореме Пифагора.
b² = c² - a²
b² = 100² - 6² = 10000 – 36 = 9964
b = √9964 ≈ 99,8
b > a
Напротив большей стороны лежит больший угол. Тогда напротив катета b лежит больший острый угол, и надо найти тангенс ∠В:
tg (∠B) = b/а = √9964/6
В ответе какое-то ненормальное число! Могу предположить, что в условии задачи есть опечатка. Например, гипотенуза с = 10, а не 100.
Тогда
b² = 10² - 6² = 100 – 36 = 64
b = √64 = 8
tg (∠B) = b/а = 8/6 = 4/3
60°
Объяснение:
Двугранный угол фи=180°÷3=60° это острый угол.