Нужна с ! известно, что точки a и b находятся на единичной полуокружности. если даны значения одной из координат этих точек, какие возможны значения другой координаты?
1. a (−8;
• такая точка не может находиться на единичной полуокружности • 8
• 0
• −8
• −1
• 1
2. b ; √3/2)
• 1/2
• такая точка не может находиться на единичной полуокружности • 0
• √2/2
• −√2/2
• 1
• −1/2
• √3/2
• −1
• −√3/2
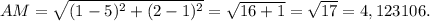
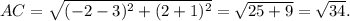
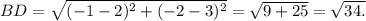
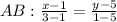
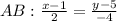
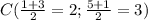
М=((-4+6)/2=1; (2+1)/2=2)
Теперь по координатам точек А и М находим длину отрезка АМ:
4) Доказательством может служить равенство диагоналей заданного четырёхугольника:
5) В этом задании неизвестно, что надо доказать.
1) Точка, равноудалённая от точек А и В, находится на перпендикуляре, проведённом к середине отрезка АВ.
Находим уравнение прямой АВ:
-4x + 4 = 2y -10
y = -2x + 7.
Находим координаты точки С - середины отрезка АВ:
Уравнение перпендикуляра у = (-1 / (-2))х + в = (1/2)х + в.
Подставим координаты точки С, находящейся на этом перпендикуляре:
3 = (1/2)*2 + в = 1 + в.
в = 3 - 1 = 2.
Уравнение перпендикуляра у = (1/2)х + 2.
При пересечении этого перпендикуляра с осью "х" значение "у" равно 0.
0 = (1/2)х + 2.
х = -2 / (1/2) = -4.
ответ: на оси абсцисс точка, равноудаленная от точек А (1; 5).,В (3; 1), имеет абсциссу -4.