Даны точки a(-1; -2; 4) b(-4; -2; 0) c(3; -2; 1)
найти:
а) вектор d=ca-cb, его модуль и направляющие косинусы, записать орт вектора d
б) скалярное произведение векторов (ca-cb)×(bc+ab)
в) векторное произведение векторов [(ca-cb)×(bc+ab)]
г) смешанное произведение векторов ([ab, cb] ca)
д) найти внутренние углы треугольника cos a, cos b, cos c
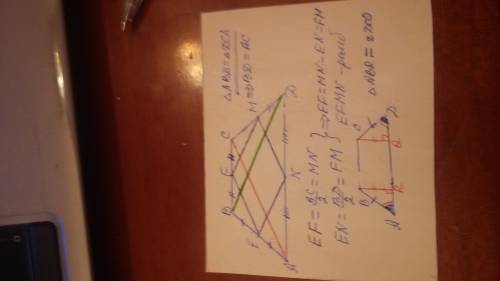
а)
б)
в)
г)
д)