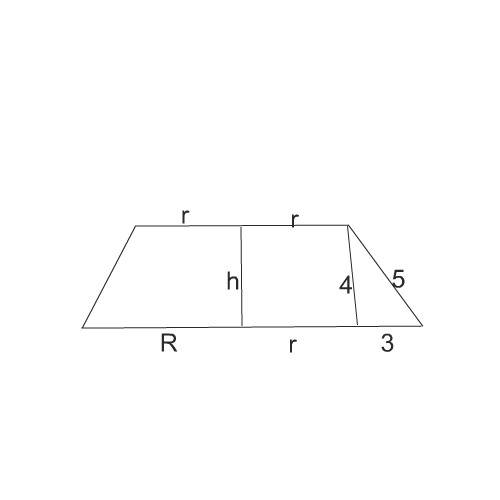
Осевое сечение этого конуса - равнобедренная трапеция. Большее основание в ней равно 2R, высота равна 4, меньшее основание найдем без вычисления, так как высота,образующая и разность радиусов оснований конуса образуют "египетский треугольник". Отсюда разность радиусов равна 3 см,
R=7 см
r=4 cм
Большее основание равно
2R=14 см
меньшее равно
2r=8см
Высота равна 4 см
Площадь трапеции (осевого сечения усеченного конуса) равна произведению высоты на полусумму оснований:
4*(14+8):2=44см²
Боковая площадь поверхности усеченного конуса вычисляется по формуле:
S=π (r1+ r2) l
(r1 - радиус нижнего основания усеченного конуса; r2 - радиус верхнего основания усеченного конуса; l - образующая усеченного конуса)
S=π (R+ r)· l=π·(7+4)·5=55π см²
1. sin <A = √ (1-cos² <A)
sin <A = √ (1-0,8²)
sin <A = 0,6
sin <A = BC / AB
0,6 = 6 / AB, AB = 10 см
по теоремі Піфагора: АС² = 10²-6²
АС = 8 см
РΔАВС = 6 + 10 + 8
РΔАВС = 24 см
2. 1 + tg² <A = 1 / cos² <A
1 + 0,75² = 1 / cos² <A
1,5625 = 1 / cos² <A
cos <A = 0,8
cos <A = AC / AB
0,8 = AC / 15
AB = 12 см
по теоремі Піфагора: ВС = √ (15²-12²), ВС = 9 см
РΔАВС = 15 + 12 + 13, Р = 40 см
3. cosA = √ (1-sin²A), cosA = 0,6
cosA = AC / AB
0,6 = 12 / AB, AB = 20 см
BC = √ ( 20²-12²), BC = 16 см
PΔABC = 20 + 12 + 16
PΔABC = 48 см
Объяснение: