Построение.
Чтобы найти точку пересечения данной прямой с плоскостью, надо найти проекции двух точек, принадлежащих этой прямой и провести через них прямую в плоскости до пересечения с данной прямой.
Объяснение:
1. Призма прямая, поэтому проекции точек А и В, принадлежащих двум боковым ребрам - это вершины основания призмы, принадлежащие этим же ребрам. Проводим прямую через вершины до пересечения с прямой АВ и получаем искомую точку С.
2 Находим проекции А' и B' точек А и В на плоскости нижнего основания. Для этого проведем прямую через любую вершину верхнего основания и точку А и прямую в плоскости нижнего основания, параллельную проведенной прямой через соответствующую вершину нижнего основания. Опустив перпендикуляр из точки А на нижнее основание до пересечения с прямой, проведенной в плоскости нижнего основания, получим проекцию A' точки А на нижнем основании. Проекция точки В на нижнем основании - соответствующая вершина нижнего основания. Проводим прямую через точки A' и B' до пересечения с прямой АВ. Получили искомую точку С.
Аналогично 3, 4 и 5. (смотри рисунок).
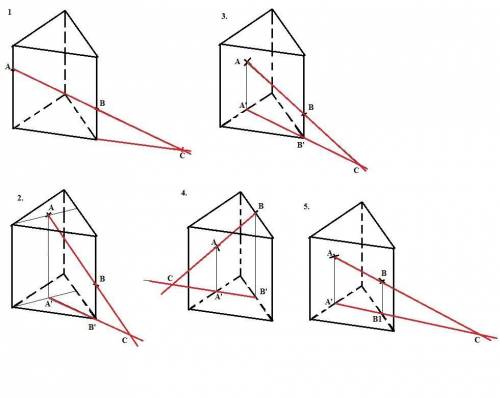
Номер 1
Можно даже не вычислять,чему равны углы 1;2;3;
Два угла 30 градусов называются соответственными,если при пересечении двух прямых секущей соответственные углы равны,то прямые параллельны
<1=<30=30 градусов,как накрест лежащие,вообще-то-смотрятс каким из двух углом сравнивать
<1+<2=180 градусов,как односторонние
<2=180-30=150 градусов
Если при пересечении двух прямых секущей односторонние углы в сумме равны 180 градусов,то прямые параллельны
<3=<2=150 градусов,как вертикальные
Номер 2
<20=<2=<20 градусов,как вертикальные
Если угол 3 в 8 раз больше угла 2,то
<3=20•8=160 градусов
<3=20+160=180 градусов
Если при пересечении двух прямых секущей односторонние углы в сумме равны 180 градусов,то прямые параллельны
<4=<3=160 градусов,как накрест лежащие
<5=<2=20 градусов
Объяснение: