Придется, наверное, использовать теорему косинусов. Площадь параллелограмма равна произведению его сторон, умноженного на синус угла между ними. Обозначим одну из сторон через a, а вторую через b. Тогда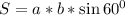 
или 
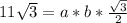. Упростив это выражение, получаем, что 
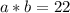. По теореме косинусов выразим наименьшую диагональ через две стороны. 
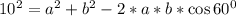. Получается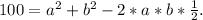 
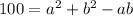так как произведение двух сторон равно 22, то 
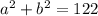Снова по теореме косинусов находится неизвестная диагональ, обозначим AC, находим через две стороны параллелограмма и угол между ними. Угол между ними равен по свойствам параллелограмма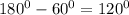 
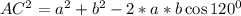, заметим, что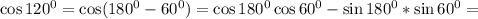 
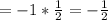
Значит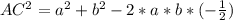 
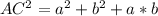
Учитывая, что 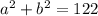и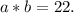 
То получается, что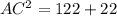 
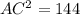Значит AC=12.
ответ: большая диагональ равна 12.
одна сторона квадрата h=b=24 - это высота призмы
смежная с ней сторона квадрата P=b=24 - это периметр основания
высота одна и та же h=b=24 - это высота призмы
в правильной треугольной призмы -
сторона основания a=P/3=b/3=24/3=8 см
площадь основания S∆= a^2√3/4=8^2√3/4=64√3/4=16√3 см2
объем призмы V∆=S∆*h=32√3h
в правильной четырехугольной призмы -
сторона основания c=P/4=b/4=24/4=6 см
площадь основания S□= c^2=6^2=36 см2
объем призмы V□=S□*h=36h
V∆ /V□ =16√3h /36h =4√3 / 9 =4√3 : 9
ОТВЕТ V∆ /V□ = 4√3 / 9 =4√3 : 9
Объяснение:
Длина любой стороны треугольника всегда меньше или равна сумме длин двух других сторон.
∠А больше∠В, т.к. ВС больше АС.
∠А больше∠С, т.к. ВС больше АВ.