
Любые две из трех прямых, соединяющих середины отрезков AB и CD; AC и BD; AD и BC могут быть:
а) параллельны одной из этих прямых.
Через две параллельные прямые можно провести плоскость, притом только одну.
б) пересекаться:
Через две пересекающиеся прямые можно провести плоскость, притом только одну.
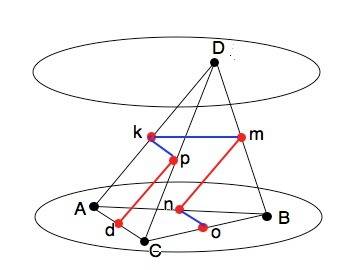
В рисунке приложения даны некоторые из получающихся пар параллельных и пересекающихся прямых:
а) pd и mn как средние линии треугольников АСD и BCD параллельны AD; kp и no параллельны основанию АС треугольников АDC и АВС.
б) km и mn, mn и no пересекаются.
Объяснение:
1)Пусть одна часть х.
Тогда ∠TSR=3x ,∠RSP=5x.
Т.к. RO-является медианой и высотой в ΔPRS, то этот треугольник равнобедренный. И значит ∠RSP=∠RPS=5х.
По т. о сумме углов треугольника для ΔТSP получаем
115+∠RPS+∠ТSР=180
5х+(5х+3х)=180-115
13х=65
х=5
∠Р=5*5=25
∠TSR=3*5=15