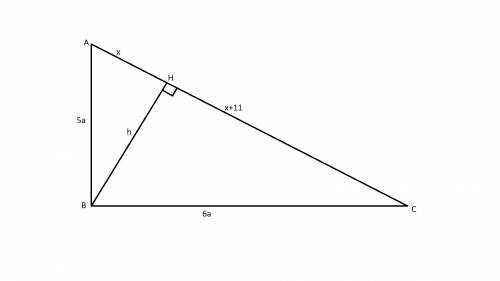
Дано:
прямоугольный треугольник АВС.
Высота из прямого угла ВН
НС=АН+11
ВС/АВ=6/5
1. Обозначим отрезок АН за х, тогда НС=х+11
По теореме Пифагора ВС²+АВ²=АС²
Выразим длины катетов через а:
ВС=6*а, АВ=5*а
(6а)² + (5а)² = (2х+11)²
61а²=(2х+11)²
2. Выразим высоту h через треугольник АВН: h²=25a²-x²
и подставим полученное значение в треугольник ВНС:
h²+(x+11)²=36a²
25a²-x² + (x²+22x+121)=36a²
сокращаем выражение и получаем: а²=2х+11
3. Подставляем выражение, полученное во втором действии в выражение, полученное в первом действии:
61(2х+11)=(2х+11)²
61=2х+11
Заметим, что 2х+11=с - гипотенуза треугольника АВС.
ответ: с=61 см.
Объяснение:
№1
Дано :
СА=40
СВ=20
угол асв =95
Найти : АВ
по теореме косинусов :
С^2=A^2+B^2-2AB * cos C
AB^2=AC^2+CB^2-2*AC*CB*cos C
AB^2=40^2+20^2-2*40*20*cos95
AB^2=1600+400-1600*(-0,08715574274)
АВ^2=2139,449188384
AB=корень из 2139,449188384
=46,25418022605092068328723287232183537
округляем до сотых : 46,25
№2
Дано:
СВ=65
угол А = 70
угол С =90
НАЙТИ : СА
tg A =BC/AC
AC=BC/tg A
AC = 65/tg 70 = 65/1.22195991814
AC=53,19323411109868108165409125029=53,2
ответ : 53,2