1)Треугольники подобны ⇒ и у другого треугольника стороныотносятся как 3х/4х/5х. Большая сторона - 5х, и она равна 15.
15=5х
х=3
тогда первая сторона 3х=9, вторая 4х=12
Периметр равен:9+12+15=36
ответ:36
2)Больший катет лежит против большего отрезка гипотенузы. По свойству катет в прямоугольном треугольнике есть среднее геометрическое между гипотенузой (16+9=25см) и его проекцией на гипотенузу (16см)
х=√(25*16)=20см
ответ:20см
3)Рисунок внизу.
В ΔABD по теореме косинусов:
cosABC=(AB²+BD²-AD²)/(2AB*BD)=(16+1-12,25)/(2*4*1)=4,75/8
В ΔABC по теореме косинусов:
AC²=AB²+BC²-2*AB*BC*cosABC=16+256-2*4*16*4,75/8=196
AC=14
ответ:14
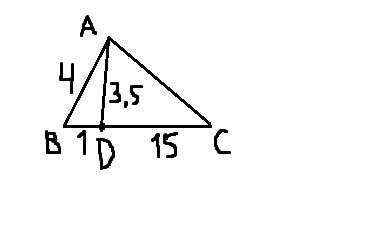
Ознаки рівності прямокутних трикутників:
Якщо гіпотенуза й катет одного прямокутного трикутника відповідно рівні гіпотенузі й катету іншого прямокутного трикутника, то такі трикутники рівні.
Якщо катети одного прямокутного трикутника відповідно рівні катетам іншого прямокутного трикутника, то такі трикутники рівні.
Якщо катет і протилежний до нього гострий кут одного прямокутного трикутника відповідно рівні катету і протилежному до нього гострому куту іншого прямокутного трикутника, то такі трикутники рівні.
Объяснение:
Площадь треугольника равна половине произведения высоты на основание, а площадь прямоугольного треугольника равна половине произведения его катетов.
Запишем это в равенстве:
1⁄2×h×c=1⁄2×b×a
Из итого следует, что:
h×c=a×b
Найдём гипотенузу (с) по теореме Пифагора:
c²=a²+b²
c²=2,4²+1²=5,76+1=6,76
c=√6,76=2,6
Теперь подставляем некоторые значения:
h×c=a×b
h×2,6=1×2,4
2,6h=2,4
h=2,4÷2,6=0,9230769230769≈0,92
ответ: h≈0,92.