Геометрия: Вычислите косинус угла между векторами а{– 4; 5} и б{5; – 4}.

Вычислите косинус угла между векторами а{– 4; 5} и б{5; – 4}.

👇

Увидеть ответ

Ответ:

Ариша03072006

17.01.2020

Объяснение:

а{– 4; 5} и b{5; – 4}.

a*b=-4*5+5*(-4)=-40

|а|=√16+25=√41

|b|=√25+16=√41

cos(a;b)=-40/(√41*√41)=-40/41

4,6(29 оценок)

Открыть все ответы

Ответ:

lera5252

17.01.2020

Угол САМ=58°

Угол АМС=58°

Угол АСМ=64°

Угол ВМК=58°

Угол МВК=64°

Угол МКВ=58°

Объяснение:

В связи с тем, что сторона АС равна стороне СМ мы понимаем, что треугольник АСМ равнобедренный.

В равнобедренном треугольнике углы при основании равны, а сумма углов треугольников равна 180°

В данном треугольнике углы при основании это угол САМ и угол АМС. Если САМ равен 58°, следовательно и угол АМС будет равен 58°

Углом при вершине в данном треуголнике является угол АСМ, он равен разности суммы углов и суммы двух других сторон, мы получаем:

180-(58+58)=64°

Перемещаемся на треугольник ВМК . Здесь, угол ВМК равен углу АМС , так как они вертикальные.

Отсюда мы получаем , что треугольники АМС и ВМК конгруэнтны.

Следовательно, угол МВК равен углу АСМ(64°), а угол МКВ равен углу САМ(58°).

4,4(41 оценок)

Ответ:

Poli4ka228

17.01.2020

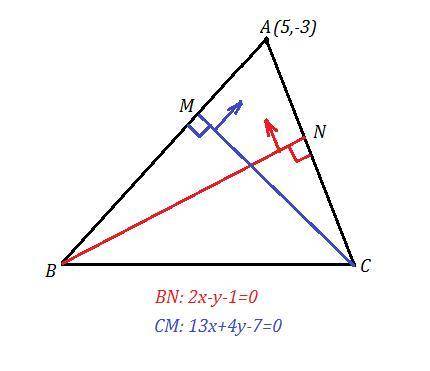
Проверим, лежит ли точка А(5,-3) на какой-либо заданной высоте. Подставим координаты этой точки в уравнения высот. Если равенство получим верное, то точка лежит на прямой.

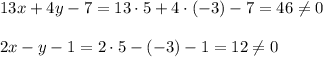
$13x+4y-7=13\cdot 5+4\cdot (-3)-7=46\ne 0\\\\2x-y-1=2\cdot 5-(-3)-1=12\ne 0$

Точка А(5,-3) не лежит ни на одной высоте. Для определённости, пусть высота BN имеет уравнение 2х-у-1=0, а высота СМ: 13х+4у-7=0.

BN⊥AC ⇒ направляющий вектор для АС равен нормальному вектору для BN: $\vec{s}_{AC}=(2,-1)$ .

Точка А(5,-3)∈АС и уравнение АС имеет вид:

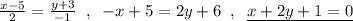
$\frac{x-5}{2}=\frac{y+3}{-1}\; \; ,\; \; -x+5=2y+6\; \; ,\; \; \underline {x+2y+1=0}$

CM⊥AB ⇒ направляющий вектор для АВ равен нормальному вектору для CМ: $\vec{s}_{AB}=(13,4)$ .

Точка А(5,-3)∈АВ и уравнение АВ имеет вид:

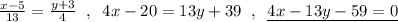
$\frac{x-5}{13}=\frac{y+3}{4}\; \; ,\; \; 4x-20=13y+39\; \; ,\; \; \underline {4x-13y-59=0}$

Координаты точки В найдём как точку пересечения АВ и BN, а координаты точки С найдём как точку пересечения АС и CM .

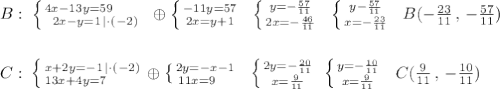
$B:\; \left \{ {{4x-13y=59\qquad } \atop {2x-y=1\, |\cdot (-2)}} \right.\oplus \left \{ {{-11y=57} \atop {2x=y+1}} \right. \; \; \left \{ {{y=-\frac{57}{11}} \atop {2x=-\frac{46}{11}}} \right.\; \; \left \{ {{y-\frac{57}{11}} \atop {x=-\frac{23}{11}}} \right. \; \; B(-\frac{23}{11}\, ,\, -\frac{57}{11})\\\\\\C:\; \left \{ {{x+2y=-1\, |\cdot (-2)} \atop {13x+4y=7\qquad }} \right.\oplus \left \{ {{2y=-x-1} \atop {11x=9\quad }} \right. \; \; \left \{ {{2y=-\frac{20}{11}} \atop {x=\frac{9}{11}}} \right.\; \left \{ {{y=-\frac{10}{11}} \atop {x=\frac{9}{11}}} \right.\; \; C(\frac{9}{11}\, ,\, -\frac{10}{11})$