Если периметр квадрата равен 24, легко найти длину одной стороны по формуле Р(кв.) = 4а, то есть 24 = 4а, получаем, что а = 6. Тогда можем воспользоваться теоремой Пифагора (т.к. у квадрата все углы прямые) и рассчитать длину диагонали как гипотенузу в прямоугольном ∆. Тогда получим, что х² = 6² + 6² = 2*36 = 72, а х = √72, то есть х = √(3² * 2² * 2) = 6√2. Мы берем только положительное значение, потому что арифметический квадратный корень ≥ 0, а длина строго больше 0. ответ: длина диагонали равна 6√2.
Из определения: прямая, параллельная плоскости, не имеет общих с плоскостью точек.отсюда следует: (1) a||b или (2) у a и b нет общих точек(скрещивающиеся). докажем (2), а заодно и опровергнем возможность пересечения. пусть a пересекает b, значит существует общая для a и b точка b, являющаяся точкой пересечения прямых. bлежит на плоскости, значит каждая точка, принадлежащая b, пренадлежитплоскости альфа (в частности в). следовательно у a и альфа есть общаяточка b, значит a не параллельна плоскости альфа по определению. противоречие. доказано - a не пересекает b.
Из условия дано PA=PB=5 см и PO = 4 см. Рассмотрим прямоугольный треугольник POA: из теоремы Пифагора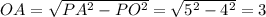 см
см
Площадь основания: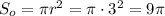 см²
см²
Объем конуса: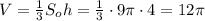 см³
см³
ответ: 12π см³.