Высота правильной треугольной пирамиды равна H, а двух гранный угол пирамиды при ее боковом ребре равен a(альфа) Найдите объем пирамиды.
Возможно есть опечатки за это не судить.
Вступление:
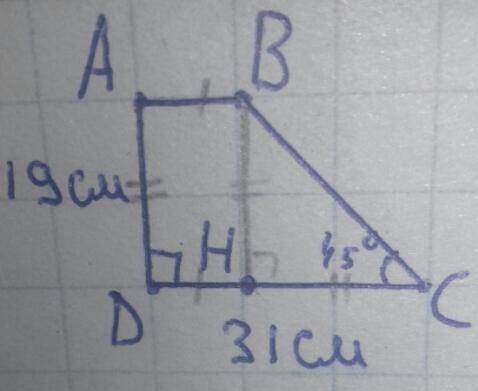
Пусть в прямоугольной трапеции ABCD, AB и CD основания, а ∠D прямой. Тогда AD меньшая боковая сторона (как расстояние между параллельными отрезками AB и CD), то есть AD=19см. По построению DC большое основание, поэтому по условию DC=31см. Острые углы при большом основании, ∠C=45° т.к. ∠D=90°.
H∈DC, BH⊥DC ⇒ BH=AD=19см.
В прямоугольном ΔBHC:
∠C=45°, ∠H=90° ⇒ ∠B=45°⇒ HC=BH=19см.
DH=DC-HC=31-19=12см.
В четырёхугольнике ABHD:
∠D=90°, ∠H=90° и ∠A=90°, ∠B=90° т.к. AB║DH, ведь H∈DC и AB║DC.
Получается ABHD - прямоугольник, поэтому AB=HD, HD=12см ⇒ AB=12см.
AB мень. осн. т.к. CD - большее.
Меньшее основание равно 12см.
* * * * * * * * * * * * * * * * * * * * * *
Высота правильной треугольной пирамиды равна H, а двугранный угол пирамиды при ее боковом ребре равен α. Найди объем пирамиды.
ответ: √3 * (3 - ctg²(α/2) ) / 4ctg² (α/2) * H ³
Объяснение:
Пусть ABC основание пирамиды , DO ее высота _ DO ⊥ пл. (ABC) . Пирамида правильная, следовательно O центр треугольника ABC. Обозначаем AB=BC=CA = a . V =(1/3)*S(ABC)*DO = (1/3)*(a²√3)/4 *H .
! Нужно вычислить только a. Покажем двугранный угол при ее боковом ребре DC (вернее линейный угол α). Поведем высоту AE треугольника ADC: AE⊥ DC и точка E соединим с B.
ΔBCE=ΔACE по первому признаку равенства: CE _общая , BC =AC и ∠BCD=∠ACD. ⇒AE=BE, ∠BEC=∠AEC =90° , т.е. еще и ∠BE⊥ DC.
Получили ∠AEB = α линейный угол двугранного угла при боковой ребре DC. Проведем высоту (медиану CM) треугольника ABC и M соединяем с вершиной D пирамиды .
--- общеизвестно O ∈ [CM] и CM=a√3 /2 и OC =(2/3)*CM=a /√3 ---
Т.к. DC⊥ EA и DC ⊥ EB ⇒ DC ⊥ пл.(AEB) ⇒ DC ⊥ EM .
! площадь треугольника MAC:
S( MAC)= (1/2)MC*DO =(1/2)DC*EM (1)
Но легко получить EM=(a/2)ctg(α/2) исходя из того что в равнобедренном треугольнике AEM медиана EM одновременно и биссектриса и высота .
(1/2)a√3 /2*H =(1/2)DC*(a/2)ctg(α/2) ⇒ DC =√3 H/ctg(α/2).
Из ΔDOC по теореме Пифагора : OC²=DС²- DO²
( a/√3) ² = (√3*H/ctg(α/2) ² - H² ⇔ a²/3= (3/ctg²(α/2) -1 )*H ²
a² =3(3 - ctg²(α/2) ) /ctg²(α/2) * H²
V = (1/3)*3(3 - ctg²(α/2) )/ctg² (α/2) √3 /4 *H³
V = √3 * (3 - ctg²(α/2) ) / 4ctg² (α/2) * H³