Если на одной из двух прямых отложить несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
Пусть дан отрезок ВС.
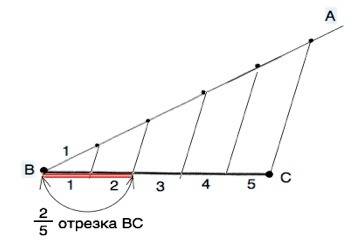
От конца В отрезка начертить луч и на нем от В отметить через равные промежутки 5 точек. Из пятой точки провести прямую через т.С отрезка ВС и провести параллельно ей прямые, пересекающие отрезок ВС. Этими прямыми ВС будет разделен на 5 равных частей. Любые две соседние части равны 2/5 исходного отрезка ВС.
* * * * * * * * * * * * * * * * * * * * * *
ответ: AD = b*tgβ*sinβ , AC = CB*tgβ = b*tgβ .
Объяснение: Решается очень разными
∡ ACD = ∡ CBD = β
( как углы со взаимно перпендикулярными сторонами )
Из ∆ACB : AC = CB*tgβ = b*tgβ .
Из ∆ADC : AD =AC*sinβ =b*tgβ*sinβ .