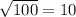Пусть трапеция АВСD. АD - ВС = 15см. Опустим из В и С высоты на АD. Тогда в полученных прямоугольных тр-ках наши высоты - равные катеты. Тогда можно написать по Пифагору: h² = 9² - X² и h² = 12² - Y², где Х+Y = 15 (разность AD и ВС). Тогда 81- X² =144- Y², откуда Y² - X² =63. Подставляем Х=15-Y и получаем: Y²-225 +30Y -Y² =63, откуда Y = 9,6см а Х = 5,4см. Косинус угла А трапеции равен Х/9, а косинус угла D трапеции равен Y/12. (так как косинус угла это отношение прилежащего катета к гипотенузе). Итак, CosA = 0,6 CosD =0,8 По таблице угол А = 53°, а угол D = 37°. Тогда угол, который образуют прямые, содержащие боковые стороны трапеции равен 180° - 53° - 37° = 90° !
1.Против угла в 30 градусов лежит катет(высота цилиндра) равный половине гипотенузы(диагонали) Высота равна 2 Найдем второй катет(диаметр круга) =6 Радиус равен 3 V=H=9*6*=54 2.Боковое ребро является гипотенузой прямоугольного треуголь ника, образованного ребром, высотой и диагональю. Если в нем один угол 60, то второй острый 30.Против 30 градусов лежит катет(1/2 диагонали) равный половине гипотенузы(ребра) 2см. Найдем высоту =2 Если половина диагонали 2 см, то вся 4см, тогда площадь основания равна 4*4/2=8кв.см V=1/3*8*2=16/3 куб.см
Объяснение:
Выполним построение треугольника ABC.
Так как треугольник ABC тупоугольный, то его высота будет опущена на продолжение треугольника ABC.
Когда мы провели высоту AD, то у нас образовалось два прямоугольных треугольника: DBC и DCK.
Так как треугольники прямоугольные, то в них будет действовать теорема Пифагора. Но нам неизвестно DC. Мы можем найти весь катет BD:
BD^2 = AB^2 - AD^2 = 17^2 - 8^2 = 225
BD =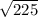 = 15
= 15
Можем найти DC: 15 - BC = 15 - 9 = 6 см
А теперь AC находим по теореме Пифагора:
AC^2 = AD^2 + DC^2 = 8^2 + 6^2 = 64 + 36 = 100
AC =