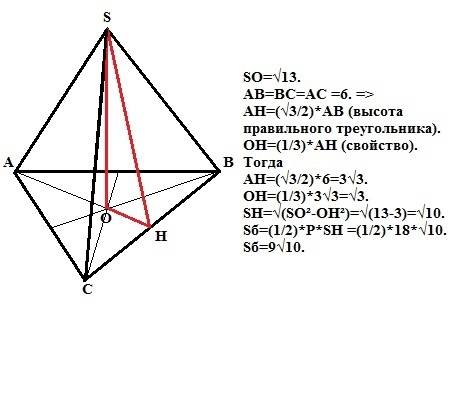
Пирамида правильная, значит ее вершина проецируется в центр основания - точку О - центр описанной и вписанной окружностей.
SO=√13 (высота пирамиды - дана).
АВ=ВС=АС =6 (стороны основания - правильного треугольника - дано).
АН=(√3/2)*АВ (формула высоты правильного треугольника).
АН - высота, биссектриса и медиана =>
ОН=(1/3)*АН (свойство медианы).
Тогда
АН=(√3/2)*6=3√3.
ОН=(1/3)*3√3=√3.
SH=√(SO²-OH²)=√(13-3)=√10.
Sб=(1/2)*Р*SH =(1/2)*18*√10 (произведение полупериметра основания на высоту боковой грани (апофему).
Sб=9√10.
(см. объяснение)
Объяснение:
Рис. 1, Рис. 2 - равны по трем сторонам. Пары: АВС, ДВС и КОN, МОN соответственно.
Рис. 3 - равны по стороне и двум прилежащим к ней углам. Пары: АFB и FBP.
Рис. 4, Рис. 5 - равны по двум сторонам и углу межлу ними. Пары: АВК, СВN и ДМВ, АМС соответственно. Примечание: рис. 4: КВ=ВN => углы при основании треугольника KBN равны; рис. 5: т.к. углы при основании треугольника AMB равны, то BM=AM и угол ДВМ=САМ.
На рисунке 6 три пары равных треугольников: ABF, ДЕС и FBC, АЕД, и АВС, АДС.