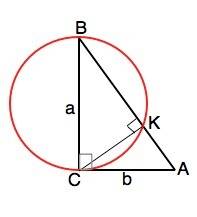
Дан прямоугольный треугольник АВС (угол С=90°). В этом треугольнике провели окружность так, что катет ВС-диаметр этой окружности. К-точка пересечения этой окружности и гипотенузы. Найти длину отрезка СК, если ВС=а, АС=b
Так как ВС - диаметр, а К - точка на окружности, то угол СКВ, опирающийся на диаметр,- прямой, и СК - высота ∆ АВС.
Воспользуемся формулой площади прямоугольного треугольника.
S=BC•AB:2
S=a•b:2
Площадь можно найти и по формуле
S=a•h:2, где а - гипотенуза, h- высота. проведенная к ней. ⇒
h=2S:AB
AB=√(BC²+AC²)=√(a²+b²)
h=ab:√(a²+b²)
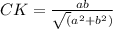
AB=5, BC=12, AC=13.
5² +12² = 25 + 144 = 169,
13² = 169. Треугольник АВС - прямоугольный, угол АВС - прямой.
Поэтому треугольник АМС лежит в вертикальной плоскости.
Проверим квадраты сторон треугольника ВМС:
ВМ=15, BC=12, МC=9.
9² +12² = 81 + 144 = 225,
15² = 225. Треугольник ВМС - прямоугольный, угол ВМС - прямой.
Угол α между плоскостями треугольника ABC и прямоугольника ABMN соответствует плоскому углу МВС.
α = arc sin(MC/BM) = arc sin(9/15) = arc sin(3/5) = 0,643501 радиан = 36,8699°.