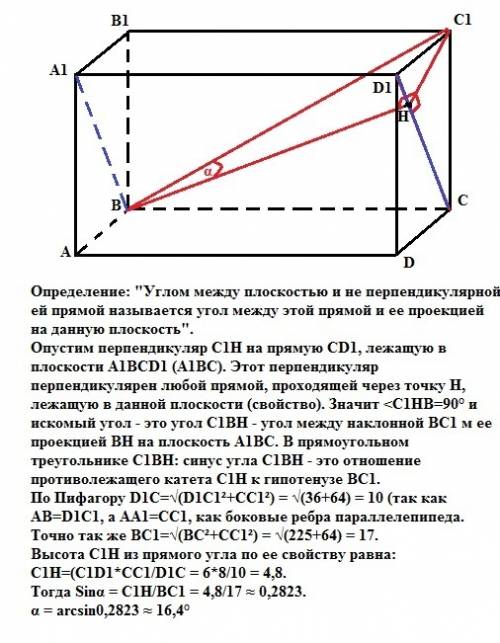
Определение: "Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость".
Опустим перпендикуляр С1Н на прямую СD1, лежащую в плоскости А1ВС (это плоскость А1ВСD1, так как секущая плоскость пересекает параллельные плоскости АА1В1В и DD1C1C по параллельным прямым А1В и D1C). Отрезок С1Н перпендикулярен любой прямой, проходящей через точку Н, лежащую в данной плоскости (свойство). Значит <C1HB=90° и искомый угол - это угол С1ВН - угол между наклонной ВС1 м ее проекцией ВН на плоскость А1ВС. В прямоугольном треугольнике С1ВН: синус угла С1ВН - это отношение противолежащего катета С1Н к гипотенузе ВС1.
По Пифагору D1C=√(D1C1²+CC1²) = √(36+64) = 10 ед (так как АВ=D1C1, a AA1=CC1, как боковые ребра параллелепипеда.
Точно так же ВС1=√(ВC²+CC1²) = √(225+64) = 17 ед.
Высота С1Н из прямого угла по ее свойству равна:
С1Н=(С1D1*CC1/D1C = 6*8/10 = 4,8 ед.
Тогда Sinα = C1H/BC1 = 4,8/17 ≈ 0,2823.
α = arcsin0,2823 ≈ 16,4°.
9
Объяснение:
Рассмотрим тр-к АВС:
угол В = 180-угА-угС=180-90-30=60
МВ-биссектриса, значит угМВС=угВ : 2=60:2=30
Рассмотрим тр-к МВС:
Гипотенуза МВ=6 (по усл)
МС - катет противолежащий углу 30
значит МС=МВ : 2=6:2=3 (по св-ву прямоугольного тр-ка с углом 30)
дополнительно проведем высоту MN на сторону АВ и рассмотрим тр-к MNB:
угNBM=угMBC=30
Гипотенуза МВ=6 (по усл)
катет MN=МВ : 2=6:2=3 (по св-ву прямоугольного тр-ка с углом 30)
Рассмотрим тр-к AMN
угА=30 (по усл)
Гипотенуза АM=МN*2=3*2=6 (по св-ву прямоугольного тр-ка с углом 30)
Имеем
АС=АМ+МС=6+3=9