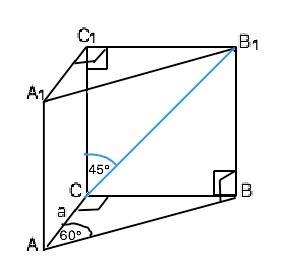
Угол АСВ=90° (дано). Призма прямая ⇒ все ее боковые грани - прямоугольники. Катет АС треугольника АВС прилежит углу 60°, ⇒ гипотенуза АВ=АС:cos60°=a:0,5=2a. Катет ВС=АВ•sin60°=2a•√3/2=a√3. В1С1 перпендикулярен плоскости АА1С1С, следовательно, перпендикулярен А1С1, а СС1 – проекция наклонной В1С. По условию ∠В1СС1=45°. Значит, В1С – биссектриса прямого угла, угол С1В1С=45°, и ∆ В1С1С - равнобедренный, поэтому высота призмы СС1=В1С1=ВС=а√3 Формула площади боковой поверхности призмы Ѕ=Р•Н (произведение периметра основания и высоты призмы). S=(а+2а+а√3)•a√3=a²•(3+√3)
1) (1;9); (5;-3); (-3;-5)
2)
Объяснение:
Решение не сложное но довольно таки ёмкое.
Рассмотрим треугольник с вершинами в заданных трёх точках. Для того чтобы четвёртая точка образовала параллелограмм с этими тремя необходимо и достаточно, чтобы эта точка была бы центрально симметрична одной из трёх данных относительно середины отрезка, концами которого являются оставшиеся две. Из чего следует, что данная задача имеет три разных решения, при условии что данные три точки не лежат на одной прямой. Определить координаты четвёртой вершины параллелограмма возможно не менее чем двумя
Находим середину одной из сторон заданного тремя вершинами треугольника и находим координаты четвёртой вершины которая будет концом отрезка чья середина совпадает с уже найденной и другим концом не использованной третей вершины заданного треугольника.
T(3;3), U(-1;2), V(1;-4); W(x₀;y₀)
I) O(x₁;y₁)-середина TU⇒x₁=(3+(-1))/2=1; y₁=(3+2)/2=2,5
O(x₁;y₁)-середина WV⇒x₁=(x₀+1)/2=1; y₁=(y₀+(-4))/2=2,5
x₀=1; y₀=9
II) O(x₁;y₁)-середина TV⇒x₁=(3+1)/2=2; y₁=(3+(-4))/2=-0,5
O(x₁;y₁)-середина WU⇒x₁=(x₀+(-1))/2=2; y₁=(y₀+2)/2=-0,5
x₀=5; y₀=-3
III) O(x₁;y₁)-середина UV⇒x₁=(-1+1)/2=0; y₁=(2+(-4))/2=-1
O(x₁;y₁)-середина WT⇒x₁=(x₀+3)/2=0; y₁=(y₀+3)/2=-1
x₀=-3; y₀=-5
параллелограмм⇔вектор AB=вектор DC
I) TUVW-параллелограмм⇔вектор TU=вектор WV
T(3;3), U(-1;2), V(1;-4); W(x₀;y₀)
TU{-1-3;2-3}={-4;-1}, WV{1-x₀;-4-y₀}
{1-x₀;-4-y₀}={-4;-1}⇒x₀=5; y₀=-3
II) TUWV-параллелограмм⇔вектор TU=вектор VW
T(3;3), U(-1;2), V(1;-4); W(x₀;y₀)
TU{-1-3;2-3}={-4;-1}, VW{x₀-1;y₀+4}
{x₀-1;y₀+4}={-4;-1}⇒x₀=-3; y₀=-5
III) TVUW-параллелограмм⇔вектор TV=вектор WU
T(3;3), U(-1;2), V(1;-4); W(x₀;y₀)
TV{1-3;-4-3}={-2;-7}, WU{-1-x₀;2-y₀}
{-1-x₀;2-y₀}={-2;-7}⇒x₀=1; y₀=9
Надеюсь, что всё понятно. Если да, то второе задание решите сами.
Используйте оба Одинаковый ответ будет подтверждением правильности ответа.