\begin{gathered} 3\cos 2x = 7\cos x \\ 3(2\cos ^{2}x - 1) - 7\cos x = 0 \\ 6\cos ^{2}x - 3 - 7\cos x = 0 \\ \cos x = t \\ 6t^{2}-7t-3=0 \\ D = 49 + 24*3 = 121 \\ \\ t_{1} = \dfrac{7 + 11}{12} = 1.5 \ ; \ \ \ t_{2} = \dfrac{7-11}{12} = -\dfrac{1}{3} \\ \\ $\left[ < br / > \begin{gathered} < br / > \cos x = 1.5 \\ \cos x = -\dfrac{1}{3} \\ < br / > \end{gathered} < br / > \right.$ \ \ \ ; \ < br / > $\left[ < br / > \begin{gathered} < br / > x \notin [-1;1] \\ x = \pm \arccos( -\dfrac{1}{3}) + 2\pi n, n \in Z < br / > \end{gathered} < br / > \right.$ \end{gathered}
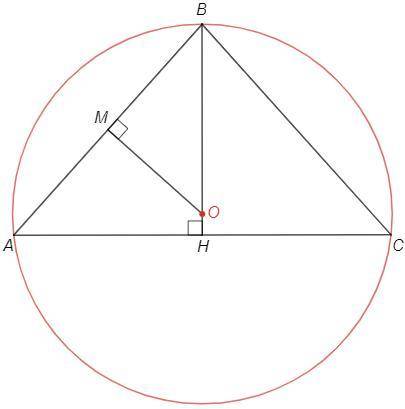
В равнобедренном треугольнике высота к основанию является также биссектрисой и медианой.
BH - высота/биссектриса/медиана
AC=4x, AB=3x
AH =AC/2 =2x
BH =√(AB^2 -AH^2) =√(9-4) x =√5 x (т Пифагора)
Центр вписанной окружности - пересечение биссектрис.
AI - биссектриса
По теореме о биссектрисе
BI/IH =AB/AH =3/2 => IH =2/5 BH =8 (см)
Центр описанной окружности - пересечение серединных перпендикуляров.
MO - серединный перпендикуляр к AB
AB/BH =3/√5 => AB =3/√5 BH =12√5
△OBM~△ABH (прямоугольные с общим углом)
OB/AB =BM/BH => OB/12√5 =6√5/20 => OB =18 (см)
Или
cosA =2/3
sinC =sinA =√(1 -cosA^2) =√5/3
AB =BH/sinA
AB/sinC =2R (т синусов) => R =BH/2sinA^2 =20/2 :(5/9) =18 (см)

Координаты АВ=(-1-4;2-(-3));Модуль АВ=Корень из(-5*-5+5*5)=Корень из 50
Объяснение: чтобы найти координаты вектора, от координаты точки конца-B(если брать АВ)отнимаем координаты точки A, модуль вектора находим с формулы:|AB|= корень из(x в квадрате + y в квадрате) x і y координаты АВ