30 см
Объяснение:
Рассмотрим вложение.
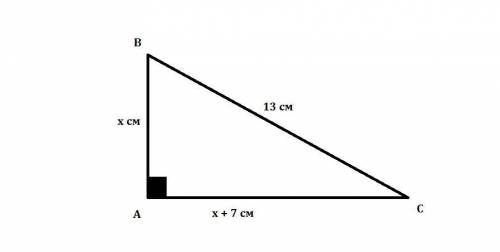
Нам дан ΔАВС: ∠А = 90°, ВС = 13 см
Пусть АВ = х см, тогда АС = х + 7 см. Воспользуемся т.Пифагора для нахождения стороны.
АВ² + АС² = ВС²
х² + (х + 7)² = 13²
х² + х² + 14х + 49 = 169
2х² + 14х + 49 - 169 = 0
2х² + 14х - 120 = 0 |:2
х² + 7х - 60 = 0
D = 7² - 4 * (-60) = 49 + 240 = 289 = 17²
x₁ = (-7 - 17)/2 = -24/2 = -12
x₂ = (-7 + 17)/2 = 10/2 = 5
т.к. сторона не может быть отрицательна, то АВ = 5 см, тогда
АС = 5 + 7 = 12 см
Чтобы найти периметр треугольника, надо сложить все стороны.
Р = АВ + ВС + АС = 5 + 13 + 12 = 30 см
Поскольку плоскость сечения параллельна оси цилиндра, сечением будет прямоугольник с высотой H, равной высоте цилиндра, и основанием длиной L, являющемся хордой, лежащей в основании цилиндра. Также известно, что диагональ прямоугольника имеет наклон в 60 градусов к его основанию. Отсюда можно записать следующие соотношения:
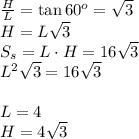
Далее проведем отрезки, соединяющие концы хорды с центром основания цилиндра. Получится равнобедренный треугольник с углом в вершине 120 градусов и бедрами, равными радиусу основания цилиндра. Проведя в этом треугольнике высоту из вешины к хорде, получим два прямоугольных треугольника, одним из катетов которых является половина хорды. Поскольку угол между этими катетами и гипотенузой равен 30 градусам, можно записать следующее соотношение между длиной хорды и радиусом основания цилиндра:
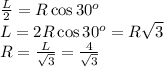
Запишем теперь выражение для площади боковой поверхности цилиндра:
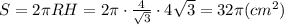
ответ: Площадь боковой поверхности цилиндра равна 32пи кв. см
Задание 1
1. Биссектриса ВЕ делит угол В на две равные части, то есть угол АВЕ равен углу СВЕ.
2. Биссектриса СД делит прямой угол С на две равные части, то есть угол АСД = 90 : 2 = 45°,
угол ВСД = 45°.
3. Выполняем расчёт величины угла СВЕ, основываясь на том, что сумма внутренних углов
треугольника СВО составляет 180°:
Угол СВЕ = 180°- 95°- 45°= 40°.
4. Острый угол В° = 40°х 2 = 80°.
5. Острый угол А = 180°- 80°- 90° = 10°.
ответ: острый угол А = 10°, острый угол В = 80°.
Задание 2.
АВС - прямоугольный треугольник, угол В = 90 градусов, угол С = 60 градусов, АВ и ВС - катеты, АС - гипотенуза.
угол А + угол В + угол С = 180 градусов (по теореме о сумме углов треугольника);
угол А + 90 + 60 = 180;
угол А = 180 - 150;
угол А = 30 градусов.
Против угла 30 градусов лежит катет, который равен половине гипотенузы, тогда:
ВС = АС/2.
Сумма гипотенузы и меньшего катета равна 42. Меньшим катетом в АВС является катет ВС, потому что на него опирается меньший угол А, поэтому:
АС + ВС = 42 см.
Получаем систему уравнений:
ВС = АС/2;
АС + ВС = 42.
Подставим первое выражение во второе вместо ВС и найдем длину гипотенузы АС:
АС + АС/2 = 42;
(2АС + АС) / 2 = 42;
3АС / 2 = 42;
3АС = 84;
АС = 84 / 3;
АС = 28 см.
ответ: АС = 28 см.