1. На данной прямой а отметим произвольную точку А.
2. Проведем окружность произвольного радиуса с центром в точке А. Точки пересечения окружности с прямой а обозначим В и С.
3. Проведем две окружности одинакового произвольного радиуса (большего половины отрезка ВС), с центрами в точках В и С.
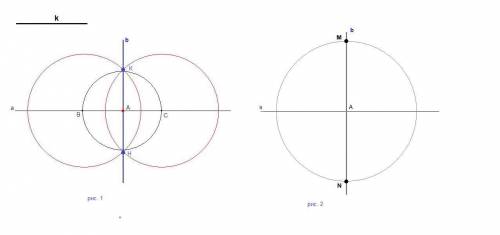
4. Через точки пересечения этих окружностей (К и Н) проведем прямую b.
Прямая b - искомый перпендикуляр к прямой а. (см. рис. 1)
5. Проведем окружность с центром в точке А с радиусом, равным данному отрезку k. Точки пересечения этой окружности с прямой b обозначим M и N. (см. рис. 2)
Точки М и N - точки, удаленные от точки пересечения прямых на расстояние, равное длине данного отрезка.
Все построение надо выполнять, конечно, на одном чертеже. Для наглядности построение последнего пункта выполнено отдельно.
Поставьте циркуль в середину основания и проведите окружность радиусом, равным медиане. Основание автоматически станет диаметром. А угол при противоположной вершине будет опираться на диаметр, то есть будет прямым, где бы вершина не находилась.
Можно и так - если достроить треугольник до параллелограма, то диагонали в нем будут равны, а это бывает только в прямоугольнике.
Можно и так - основание медианы равноудалено от вершин треугольника, значит, оно лежит на перпендикуляре, проходящем через середину стороны (любой, к которой медиана НЕ проведена). То есть средняя линяя треугольника перпендикулярна другой стороне. То есть треугольник прямоугольный.