Объяснение:
Тангенс угла в прямоугольном треугольнике - это отношение противолежащего катета к прилежащему. Проведём дополнительные прямые линии так, чтобы получить прямоугольные треугольники, из которых можно будет найти катеты необходимых углов и воспользуемся формулами тангенса суммы и разности углов.
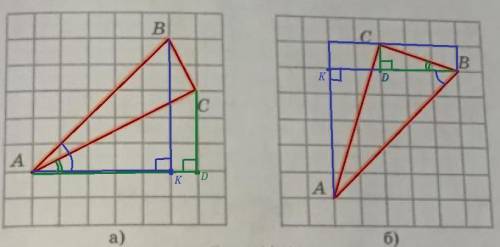
а)
tg∠A = BC / AC = 3/6 = 1/2
ctg∠A = AC / BC = 6/3 = 2
б)
tg∠B = AC / BC = 4/6 = 2/3
ctg∠B = BC / AC = 6/4 = 3/2
№2
Тангенс угла в прямоугольном треугольнике -это отношение противолежащего катета к прилежащему. Проведём дополнительные прямые линии так, чтобы получить прямоугольные треугольники, из которых можно будет найти катеты необходимых углов и воспользуемся формулами тангенса суммы и разности углов.
tg(a-β)=tga-tgβ/1+tga×tgβ; tg(a+β)= tga+tgβ/1-tga×tgβ
a)tg ∠BAC = tg(∠BAD-∠CAD) =tg∠BAD- tg-∠CAD/1+tg∠BAD×tg∠CAD=∠BAD= BK/AK=5/5=1; tg∠CAD= CD/AD=3/6=1/2=1-1/2/1+1×1/2=1/2/3/2=1/3
ctg∠BAD=1/tg∠BAD=1/1/3
b) tg∠ABC=tg(∠CBD+∠KBA) =tg∠CBD+tg∠KBA/1-tg∠CBD×tg∠KBA=tg∠CBD=CD/BD=1/3; tg∠KBA=AK/BK=5/5=1=1/3+1/1-1×1/3=4/3/2/3=4/2=2
В равнобедренном треугольнике с периметром 32 см длина отрезка, соединяющая середины боковых сторон, равна 6 см. Найдите диаметр окружности, вписанной в этот треугольник
Объяснение:
Т.к. средняя линия 6 см , то основание 12 см , по т. о средней линии.
Тогда равные боковые стороны (32-12):2=10 ( см).
d=2r , а радиус можно найти из формулы S=1/2*P*r.
Площадь треугольника можно найти по ф. Герона ,
р=32:2=16 , р-а=16-10=6, р-в=16-10=6 , р-с=16-12=4,
S=√( 16 *6*6*4)=4*6*2=48 (см²)
S=1/2*P*r , 48=1/2*32*r , r=3 см ⇒ d=6 см
Формула Герона S= √p (p−a) (p−b) (p−c) , полупериметр p= 1 ÷2 *(a+b+c).